1. Тип 13 № 500000 
Классификатор алгебры: Однородные тригонометрические уравнения, Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Уравнения. Тригонометрические уравнения, сводимые к однородным
i
Дано уравнение 
а) Решите данное уравнение.
б) Укажите корни данного уравнения, принадлежащие промежутку 
Решение. а) Сведем уравнение к квадратному относительно тангенса:
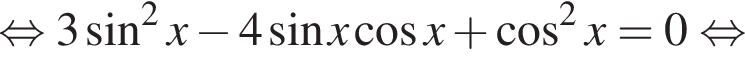
б) С помощью числовой окружности находим, что из найденных решений промежутку принадлежат числа 
Ответ: а) 
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
500000
а) б)
б) Классификатор алгебры: Однородные тригонометрические уравнения, Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
то из уравнения следует, что 
что противоречит основному тригонометрическому тождеству. Поэтому 
отличен от 0, на него можно поделить обе части уравнения:
и 
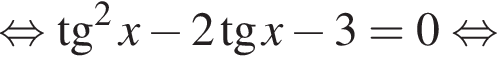
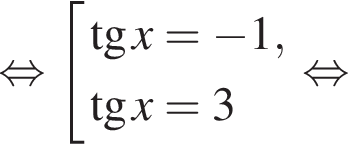
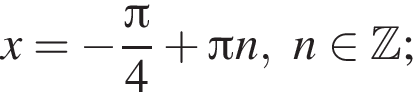
б) 
б) 
заменим выражение в скобках на 
получаем однородное тригонометрическое уравнение первой степени:
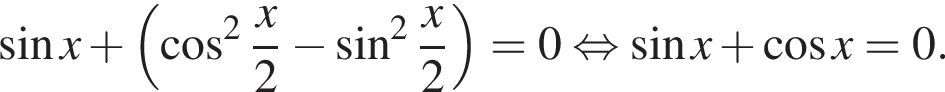
то из уравнения следует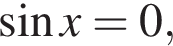 
что невозможно в силу основного тригонометрического тождества. Значит, на множестве корней уравнения 
Разделим обе части уравнения на 
откуда 
Следовательно, 
Поэтому на данном отрезке получаем единственный корень 
б) 
и 
б) 
получим кубическое уравнение относительно тангенса:
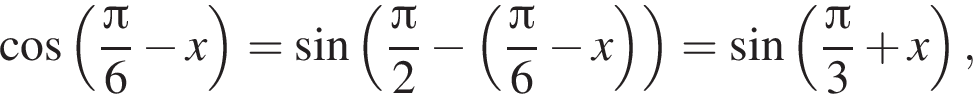
и решим его методом группировки: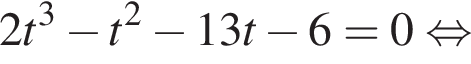
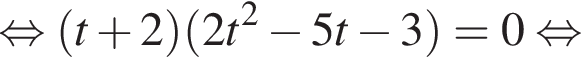
откуда 
соответственно.
лежат числа 
и 
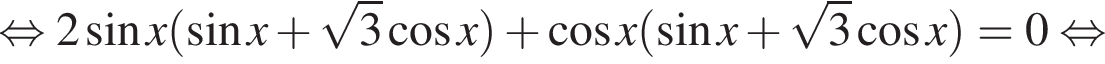
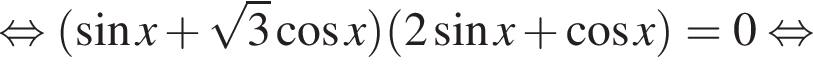
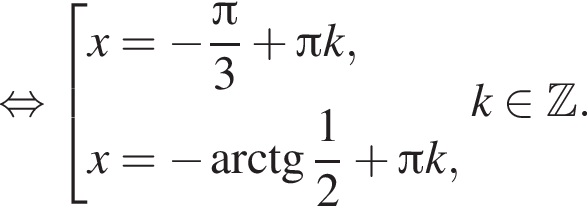
б) 
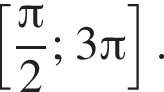
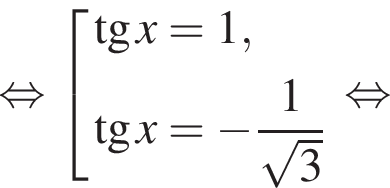
б) 
б) 
поэтому преобразование 
и преобразуем уравнение:
Рассмотрим вторую серию: заметим, что 
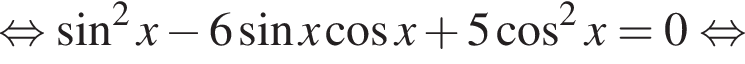
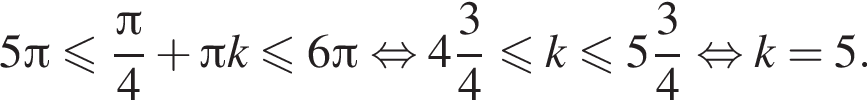
тогда
