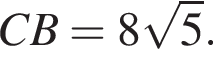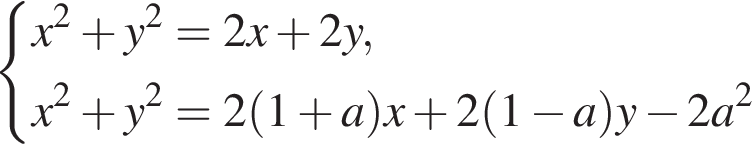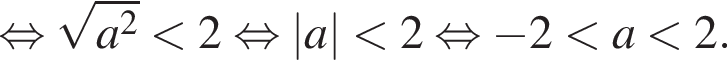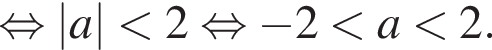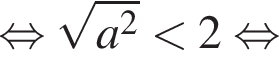1. Тип 13 № 548851 

Источники:
Классификатор алгебры: Область определения уравнения, Сравнение чисел, Тригонометрические уравнения
Методы алгебры: Введение замены, Сведение к однородному
Уравнения. Тригонометрические уравнения, сводимые к квадратным
i
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение. а) Пусть  тогда уравнение запишется в виде
тогда уравнение запишется в виде  откуда t = 1 или t = −2. Далее имеем:
откуда t = 1 или t = −2. Далее имеем:

б) Корни отберем с помощью тригонометрической окружности (см. рис.). На отрезке  лежат числа
лежат числа 
Ответ: а) 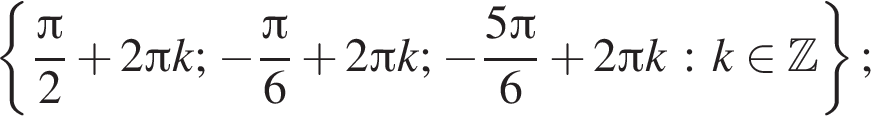 б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а) 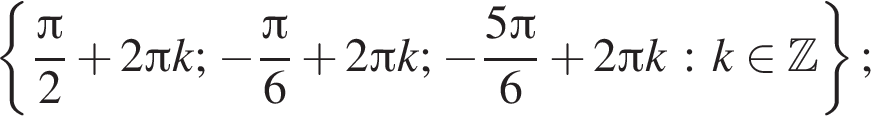 б)
б) 
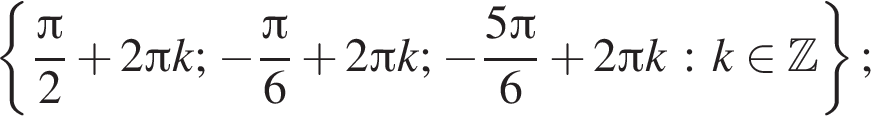 б)
б) 
548851
а) 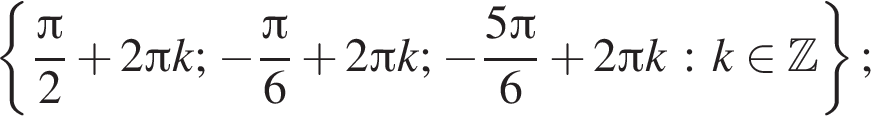 б)
б) 
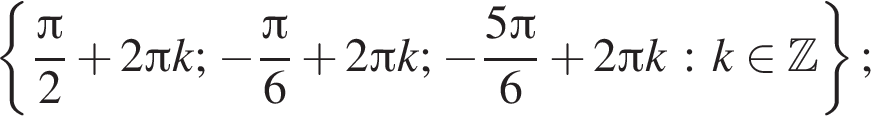 б)
б) 
Классификатор алгебры: Область определения уравнения, Сравнение чисел, Тригонометрические уравнения
Методы алгебры: Введение замены, Сведение к однородному
 Что и требовалось доказать.
Что и требовалось доказать.




















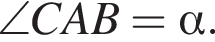 Треугольник ANC равнобедренный, поэтому
Треугольник ANC равнобедренный, поэтому  и
и  Треугольник CLN также равнобедренный, поэтому
Треугольник CLN также равнобедренный, поэтому Вычислим
Вычислим  как внешний угол в треугольнике LMC:
как внешний угол в треугольнике LMC:



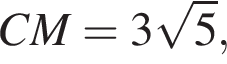

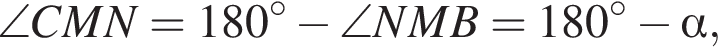









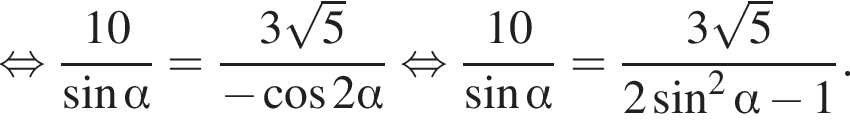


 тогда
тогда


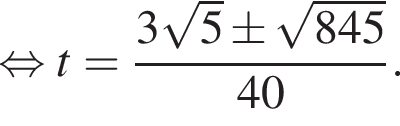
 поэтому
поэтому 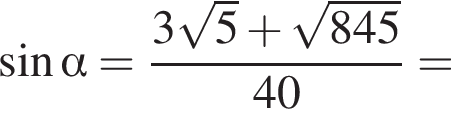






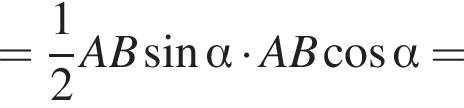

 поэтому дуга AL равна 90°. На эту дугу опирается центральный угол ANL, тогда
поэтому дуга AL равна 90°. На эту дугу опирается центральный угол ANL, тогда  Углы ANL и MNB равны как вертикальные, таким образом,
Углы ANL и MNB равны как вертикальные, таким образом,  тогда треугольники ABC и MNB подобны по двум углам. Следовательно,
тогда треугольники ABC и MNB подобны по двум углам. Следовательно, 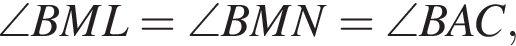 что и требовалось доказать.
что и требовалось доказать.



 тогда
тогда