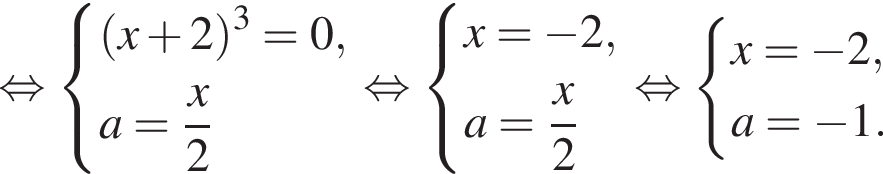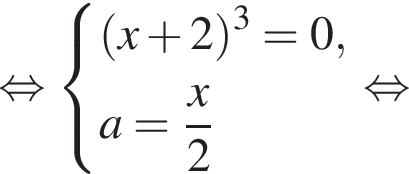1. Тип 13 № 528341 

Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ:
Уравнения. Тригонометрия и логарифмы
i
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 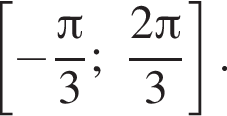
Решение. a) Пусть  тогда имеем:
тогда имеем:
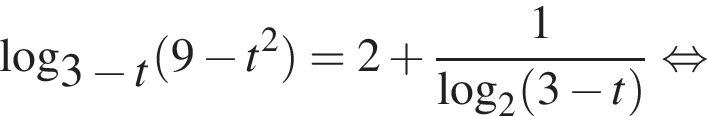

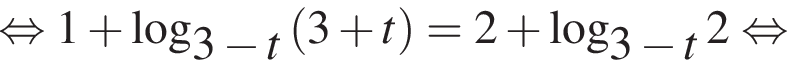

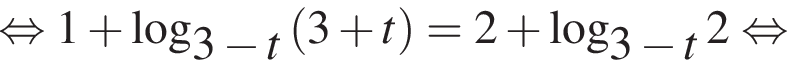

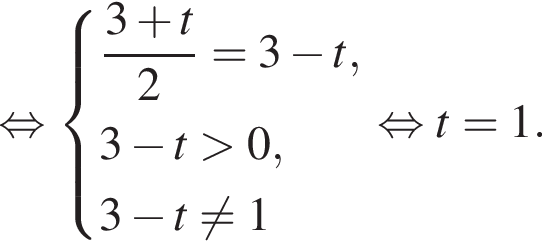
Вернёмся к исходной переменной:

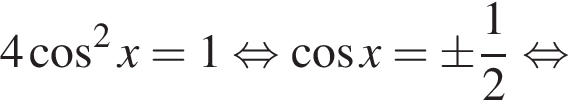

б) При помощи единичной окружности отберём корни, лежащие на отрезке 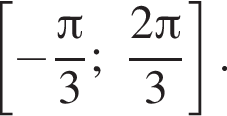 Получаем числа
Получаем числа 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
528341
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ:






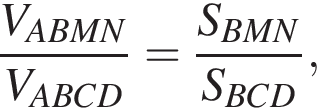 так как высоты этих пирамид, опущенные из вершины A, совпадают. Таким образом,
так как высоты этих пирамид, опущенные из вершины A, совпадают. Таким образом,  При этом, по теореме об отношении площадей треугольников с равным углом,
При этом, по теореме об отношении площадей треугольников с равным углом, 
 то есть
то есть 
 из п. а) находим, что
из п. а) находим, что  Вычислим объём ABMN третьим способом:
Вычислим объём ABMN третьим способом:
 Пусть угол между плоскостями ABC и AMN равен α. Заметим, что треугольник AMB есть проекция треугольника AMN на плоскость ABC. Тогда
Пусть угол между плоскостями ABC и AMN равен α. Заметим, что треугольник AMB есть проекция треугольника AMN на плоскость ABC. Тогда  откуда
откуда 


 тогда имеем:
тогда имеем:






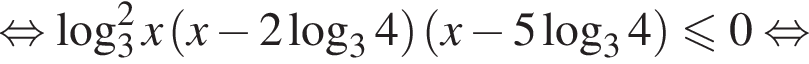



 Положим
Положим  тогда
тогда 


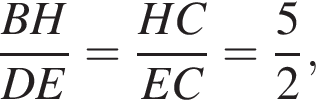 откуда
откуда  что и требовалось доказать.
что и требовалось доказать.
 откуда
откуда 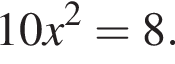 Тогда:
Тогда:


 откуда
откуда  Треугольники BMD и BHC подобны, следовательно,
Треугольники BMD и BHC подобны, следовательно, 

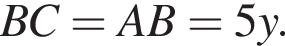 Треугольник ABD — прямоугольный, тогда
Треугольник ABD — прямоугольный, тогда

















 Тогда сумма выплат равна
Тогда сумма выплат равна 









 тыс. руб.
тыс. руб. получаем:
получаем: