Ребро SA пирамиды SABC перпендикулярно плоскости основания ABC.
а) Докажите, что высота пирамиды, проведённая из точки A, делится плоскостью, проходящей через середины рёбер AB, AC и SA, пополам.
б) Найдите расстояние от вершины A до этой плоскости, если 
AB = AC = 5, 
Решение. а) Пусть AH — искомая высота. Проведем прямую SH, обозначим K точку пересечения прямой SH со стороной основания BC. Проведем прямую AK. Точки T и N — середины сторон AC и AB, поэтому отрезок TN — средняя линия треугольника ABC. Следовательно, TN делит отрезок AK на две равные части. Поэтому MF — средняя линия треугольника SKA, она делит AH на две равные части.
б) По условию AB = AC, поэтому треугольник ABC — равнобедренный. Поскольку SC = SB, треугольник SCB тоже равнобедренный. Ребро SA перпендикулярно плоскости основания пирамиды, поэтому оно перпендикулярно и стороне основания AB. Тогда прямоугольные треугольники SAC и SAB равны по двум катетам.
Так как AC = AB, AH ⊥ (CBS), следовательно, HC ⊥ AH, AH ⊥ HB, тогда HC = HB. Значит, точка H принадлежит серединному перпендикуляру к CB, то есть SK, так как SK — медиана, высота и биссектриса равнобедренного треугольника. Тогда 
AK — биссектриса, медиана и высота равнобедренного треугольника ABC. По теореме Пифагора AK = 
Поскольку SA ⊥ (ABC), SA ⊥ AK. Тогда по теореме Пифагора SK = 5. Далее, 
то есть SH = 1, следовательно, из треугольника SAH по теореме Пифагора AH = 2. Тогда искомое расстояние равно 1.
Ответ: б) 1.
Решим пункт б) методом объёмов (Денис Чернышёв, Тюмень).
Объем пирамиды можно выразить двумя способами: 
и 
Приравнивая объемы, получаем
а значит, 
Осталось найти площади треугольников ABC и SCB.
В равнобедренном треугольнике ABC по теореме Пифагора находим высоту
откуда получаем площадь:
Высоту треугольника SCB найдем из прямоугольного треугольника 
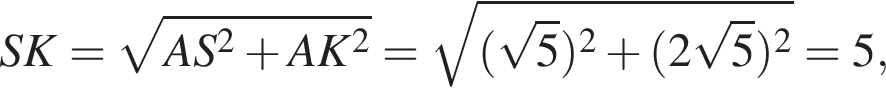
тогда
Следовательно, 
Таким образом, по доказанному в п. а), искомое расстояние равно 1.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Тогда 
Высота LB правильного треугольника ABC равна 
По теореме косинусов 
то есть 
По теореме, обратной теореме Пифагора, треугольник CA1D прямоугольный. Тогда CD ⊥ CA1. Поскольку С1D1 || CD, имеем C1D1 ⊥ CA1.
Тогда, по теореме о площади проекции, площадь искомого сечения 
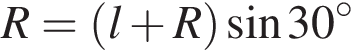и 
Имеем 
По теореме косинусов в треугольнике KOO1 имеем:
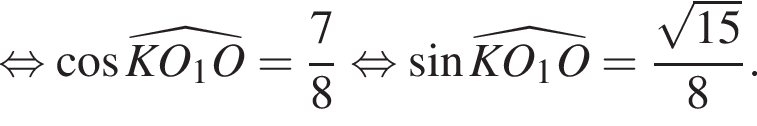
Поскольку треугольник MOT — прямоугольный, то OM — высота и медиана в треугольнике KO1T. Таким образом, KT = 2KM = 15.
и 
Поскольку 
находим: 
Также имеем 
Заметим, что треугольники AB1B и BCB1 имеют общую высоту, следовательно: 
Поэтому 
Аналогично доказываем, что 
Тогда 
из которого, в свою очередь, следует параллельность отрезков BC и 
Отрезок 
рассекает исходный треугольник ABC на треугольник 
и трапецию 
в которой точка О — это точка пересечения диагоналей.
тогда 
составит 
Диагонали трапеции отсекают от неё подобные треугольники BCO и 
в которых 
Поэтому площадь 
а площадь треугольника 
составит его 25-ю часть, то есть 
Наконец, 
и 
тогда CM = 
(так как 
) 
то есть 
Тогда из подобия треугольников ABH и AMT, получаем, MT =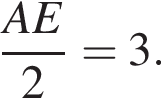 
Тогда MP = 
Тогда 
По теореме Пифагора 
Аналогично получаем, что 
тогда по теореме косинусов 
DK.
то есть DH = 50, тогда HK = 288. Значит, 
Тогда MH = 120 + 169 = 289.