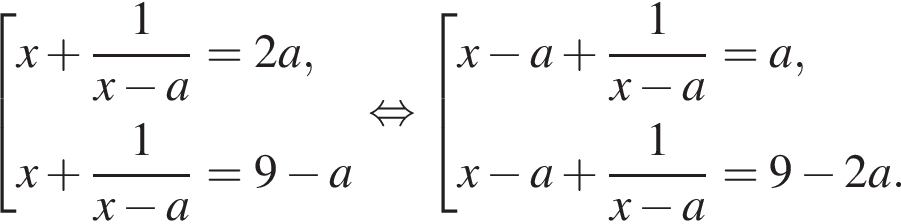Найдите все значения a, при которых уравнение






имеет ровно два решения.
Решение. Пусть  тогда уравнение запишется в виде
тогда уравнение запишется в виде  откуда
откуда  или
или  Значит, решения исходного уравнения — это решения одного из уравнений
Значит, решения исходного уравнения — это решения одного из уравнений  или
или 
Исследуем, сколько решений имеет уравнение  в зависимости от a и b. При
в зависимости от a и b. При ![]() уравнение принимает вид
уравнение принимает вид  Это квадратное уравнение, дискриминант которого равен
Это квадратное уравнение, дискриминант которого равен  Таким образом, уравнение
Таким образом, уравнение  имеет два решения при
имеет два решения при  одно решение при
одно решение при  и не имеет решений при
и не имеет решений при  При
При ![]() уравнение принимает вид
уравнение принимает вид  и имеет одно решение.
и имеет одно решение.
Уравнение  и
и  совпадают при
совпадают при  то есть при
то есть при ![]() В этом случае мы получаем единственное уравнение
В этом случае мы получаем единственное уравнение  которое имеет два решения.
которое имеет два решения.
При других значениях a исходное уравнения имеет ровно два решения, если либо оба уравнения  и
и  имеют по одному решению, либо одно из них не имеет решений, а другое имеет два решение. При
имеют по одному решению, либо одно из них не имеет решений, а другое имеет два решение. При ![]() каждое из этих уравнений имеет единственное решение и эти решения различны. При других значениях a выполнено неравенство
каждое из этих уравнений имеет единственное решение и эти решения различны. При других значениях a выполнено неравенство  поэтому уравнение
поэтому уравнение  имеет два решения. А значит, уравнение
имеет два решения. А значит, уравнение  не должно иметь решений. Это выполнено при
не должно иметь решений. Это выполнено при  то есть при
то есть при  и при
и при ![]()
Таким образом, исходное уравнение имеет ровно два решения при 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 4 |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точек  и/или и/или | 3 |
C помощью верного рассуждения получен один из промежутков множества значений a:  или или  возможно, с включением граничных точек. возможно, с включением граничных точек. | 2 |
| Верно найдено хотя бы одно из значений a: ИЛИ Верно найдена хотя бы одна из граничных точек множества значений a: ИЛИ Получено хотя бы одно из уравнений | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |





 ровно два решения.
ровно два решения. тогда уравнение запишется в виде
тогда уравнение запишется в виде  откуда
откуда  или
или  Значит, решения исходного уравнения — это решения уравнений
Значит, решения исходного уравнения — это решения уравнений  или
или 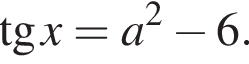
 в зависимости от b. На промежутке
в зависимости от b. На промежутке  функция
функция  принимает каждое неотрицательное значение один раз, на промежутке
принимает каждое неотрицательное значение один раз, на промежутке  функция
функция  могут иметь общие решения при
могут иметь общие решения при  то есть при
то есть при  При
При  и имеют два решения на отрезке
и имеют два решения на отрезке  При
При 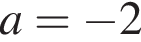 оба уравнения принимают вид
оба уравнения принимают вид  и имеют одно решение на отрезке
и имеют одно решение на отрезке  если оба уравнения
если оба уравнения 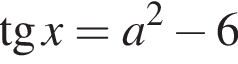 имеют по одному решению. Получаем систему неравенств:
имеют по одному решению. Получаем систему неравенств:


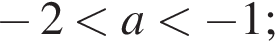

 и/или
и/или 
 множества значений a, возможно, с с включением граничных точек и/или исключением точки
множества значений a, возможно, с с включением граничных точек и/или исключением точки 




 тогда неравенство запишется в виде
тогда неравенство запишется в виде



 нам требуется найти все значения a, при которых неравенство выполнено при
нам требуется найти все значения a, при которых неравенство выполнено при 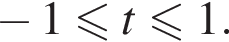
 и
и  Функция
Функция  возрастающая. Таким образом, если неравенство
возрастающая. Таким образом, если неравенство 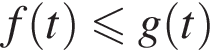 выполнено при
выполнено при  то оно выполнено при
то оно выполнено при 
 неравенство принимает вид
неравенство принимает вид

 и больше нуля при других значениях a. Выражение
и больше нуля при других значениях a. Выражение  при
при  принимает вид
принимает вид  при
при  выполнено при
выполнено при 

 множества значений a, возможно, с исключением точки
множества значений a, возможно, с исключением точки 




 тогда неравенство запишется в виде
тогда неравенство запишется в виде

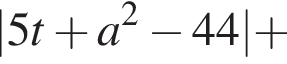

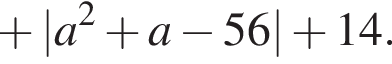
 необходимо найти все значения a, при которых неравенство выполнено при
необходимо найти все значения a, при которых неравенство выполнено при  и
и  Функция
Функция  убывающая. Таким образом, если неравенство
убывающая. Таким образом, если неравенство  а значит, и на отрезке
а значит, и на отрезке 



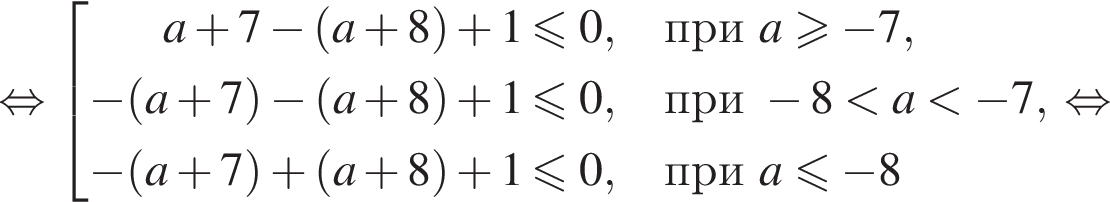



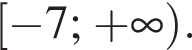
 и/или
и/или  множества значений a, возможно, с исключением точки
множества значений a, возможно, с исключением точки 





 При
При  правая часть уравнения
правая часть уравнения  При
При  правая часть уравнения равна 4, а левая часть уравнения не меньше 4, причём равенство достигается только при
правая часть уравнения равна 4, а левая часть уравнения не меньше 4, причём равенство достигается только при  Значит, исходное уравнение имеет единственное решение
Значит, исходное уравнение имеет единственное решение  Числа −2, 0 и 2 являются корнями этого уравнения.
Числа −2, 0 и 2 являются корнями этого уравнения.

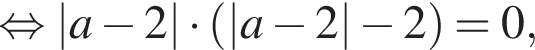
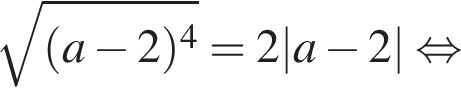

 левая часть уравнения не меньше 4, причём равенство достигается только при x = 0. При x > 2 правая часть уравнения
левая часть уравнения не меньше 4, причём равенство достигается только при x = 0. При x > 2 правая часть уравнения  но дальнейшие рассуждения неверны или отсутствуют.
но дальнейшие рассуждения неверны или отсутствуют.

 возрастает на области определения и принимает все значения от
возрастает на области определения и принимает все значения от  имеет единственное решение. Это решение принадлежит отрезку
имеет единственное решение. Это решение принадлежит отрезку  и
и  Получаем систему неравенств:
Получаем систему неравенств:







 возрастает на области определения и принимает все значения от
возрастает на области определения и принимает все значения от  Получаем систему неравенств:
Получаем систему неравенств: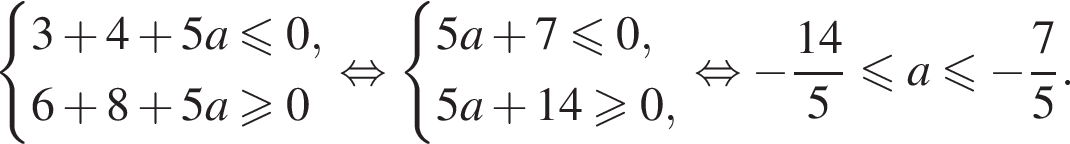









 тогда, используя теорему, обратную теореме Виета, получим:
тогда, используя теорему, обратную теореме Виета, получим:

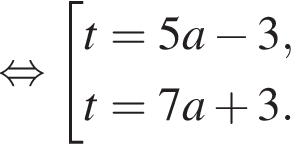
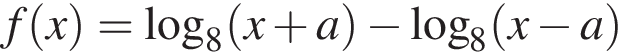 имеет с горизонтальными прямыми
имеет с горизонтальными прямыми  и
и  ровно две общие точки. Эти прямые совпадают, если
ровно две общие точки. Эти прямые совпадают, если 
 имеем:
имеем:





 откуда
откуда  при
при  откуда
откуда 
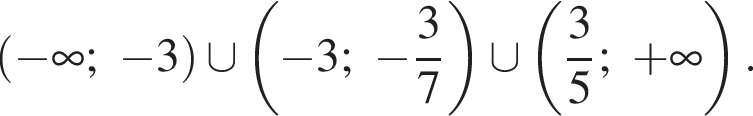



 или
или 
 в зависимости от a и
в зависимости от a и 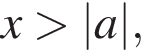 левая часть определена и принимает вид
левая часть определена и принимает вид
 выражение
выражение  принимает по одному все значения из промежутка
принимает по одному все значения из промежутка  для
для  принимает по одному разу все значения из промежутка
принимает по одному разу все значения из промежутка  при
при  при
при  и не имеет решений при
и не имеет решений при  При
При  и
и  могут иметь общие решения при
могут иметь общие решения при  то есть при
то есть при  оба уравнения принимают вид
оба уравнения принимают вид  и имеют одно решение.
и имеют одно решение.
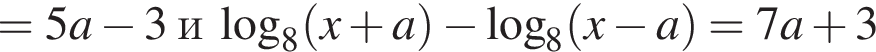

 и/или
и/или 
 или
или 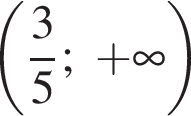 ; возможно, с включением граничных точек и/или исключением точки
; возможно, с включением граничных точек и/или исключением точки 
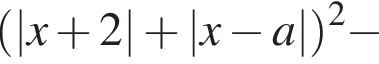



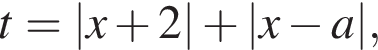 тогда исходное уравнение принимает вид:
тогда исходное уравнение принимает вид:

 или
или  Исследуем сколько решений имеет уравнение
Исследуем сколько решений имеет уравнение  в зависимости от a и
в зависимости от a и 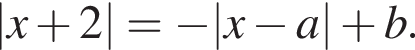 График левой части этого уравнения — график модуля с вершиной в точке
График левой части этого уравнения — график модуля с вершиной в точке  график правой части — график модуля, отражённый относительно
график правой части — график модуля, отражённый относительно  лежит правее (выше) прямой
лежит правее (выше) прямой  и прямая
и прямая  лежит левее (выше) прямой
лежит левее (выше) прямой  Это достигается условиями
Это достигается условиями  и
и  Таким образом, уравнение совокупности имеет два решения при условии:
Таким образом, уравнение совокупности имеет два решения при условии:
 то уравнение имеет два решения, если прямые
то уравнение имеет два решения, если прямые  и
и  или
или  или
или 

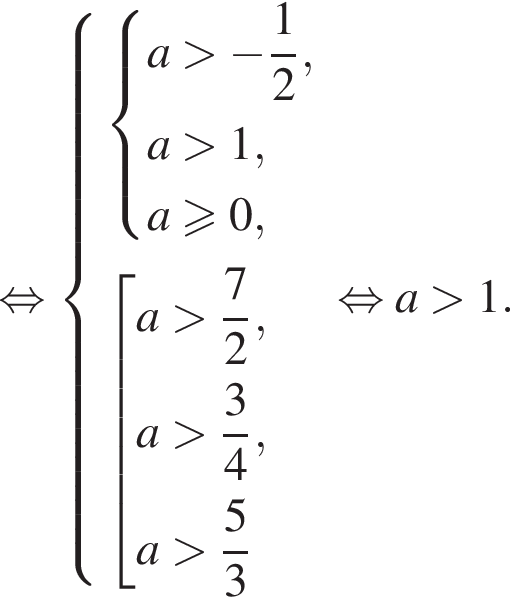
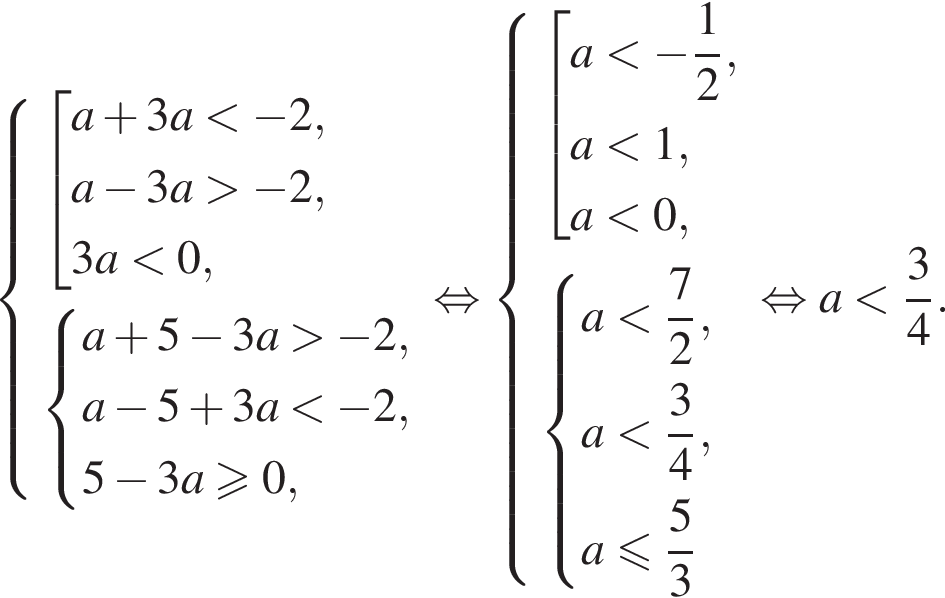


 откуда
откуда  При данном значении a оба уравнения принимают вид:
При данном значении a оба уравнения принимают вид: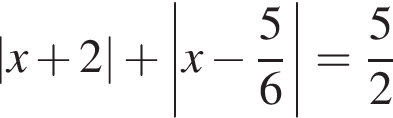

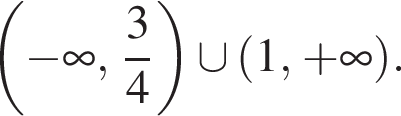


 и
и  и
и 
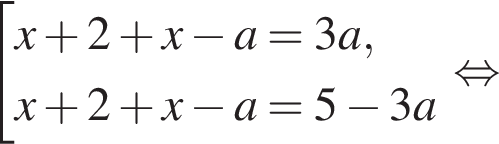

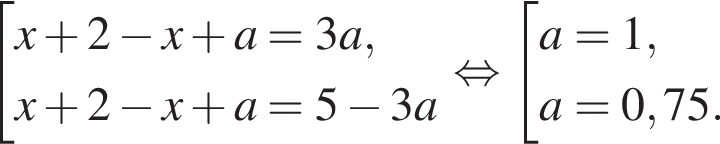
 и
и 
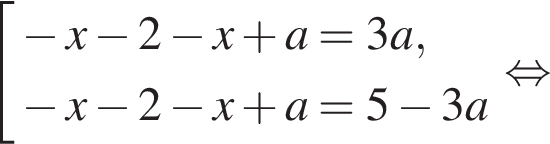


 или
или  или
или  исходное уравнение не имеет решений.
исходное уравнение не имеет решений.
 .
.



 тогда исходное уравнение принимает вид:
тогда исходное уравнение принимает вид:
 (2)
(2) или
или 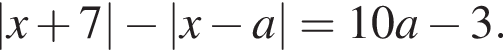 Исследуем сколько решений имеет уравнение
Исследуем сколько решений имеет уравнение  в зависимости от a и
в зависимости от a и  Левая часть этого уравнения — график модуля с вершиной в точке
Левая часть этого уравнения — график модуля с вершиной в точке  график правой части — график модуля, с вершиной в точке
график правой части — график модуля, с вершиной в точке  и прямая
и прямая  либо, если одновременно прямая
либо, если одновременно прямая  Получаем совокупность двух систем уравнений:
Получаем совокупность двух систем уравнений: (3)
(3)






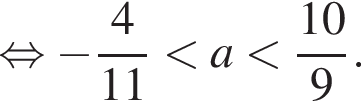
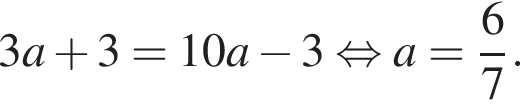


 .
.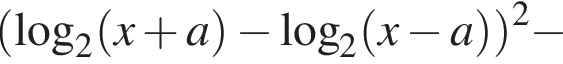

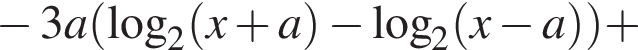

 тогда получим:
тогда получим:
 или
или 
 в зависимости от a и
в зависимости от a и 
 принимает по одному разу все значения из промежутка
принимает по одному разу все значения из промежутка  и
и  могут иметь общие решения при
могут иметь общие решения при  то есть при
то есть при 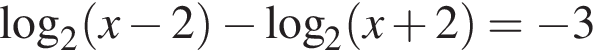 и имеют одно решение.
и имеют одно решение. и
и  имеют по одному решению. Получаем систему неравенств:
имеют по одному решению. Получаем систему неравенств:

 или
или 



 тогда уравнение запишется в виде
тогда уравнение запишется в виде


 или
или 
 в зависимости от a и
в зависимости от a и 
 принимает по одному разу все значения из промежутка
принимает по одному разу все значения из промежутка  и
и  могут иметь общие решения при
могут иметь общие решения при  то есть при
то есть при 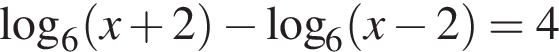 и имеют одно решение.
и имеют одно решение.




 или
или  ; возможно, с включением граничных точек и/или исключением точки
; возможно, с включением граничных точек и/или исключением точки 





 тогда исходное уравнение записывается в виде
тогда исходное уравнение записывается в виде  Функция f возрастает, поскольку является суммой двух возрастающих функций. Монотонная функция принимает все свои значения единожды, поэтому получаем:
Функция f возрастает, поскольку является суммой двух возрастающих функций. Монотонная функция принимает все свои значения единожды, поэтому получаем:
 принимает значения от
принимает значения от  монотонно возрастает на отрезке
монотонно возрастает на отрезке  и принимает на нём значения от
и принимает на нём значения от  а с ним и исходное уравнение имеют решение при
а с ним и исходное уравнение имеют решение при 






 равна
равна 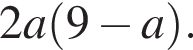 Поэтому корни — суть числа
Поэтому корни — суть числа