Тип Д15 C4 № 508667 

Сложная планиметрия. Треугольники
i
В равнобедренном треугольнике ABC (AB = BC) проведены биссектрисы AK, BM, CP.
а) Докажите, что треугольник KMP — равнобедренный.
б) Найдите площадь треугольника KMP, если известно, что площадь треугольника ABC равна 64, а косинус угла ВАС равен 0,3.
Решение. 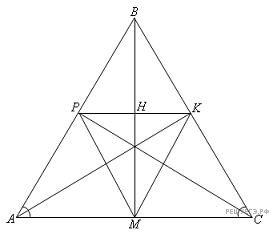 а) Известно, что прямая, содержащая биссектрису равнобедренного треугольника, проведенную к его основанию, является осью его симметрии.
а) Известно, что прямая, содержащая биссектрису равнобедренного треугольника, проведенную к его основанию, является осью его симметрии.
Рассмотрим  и
и  У них:
У них:  — общий, AB = CB,
— общий, AB = CB,  как половины равных углов при основании равнобедренного треугольника. Значит,
как половины равных углов при основании равнобедренного треугольника. Значит,  по второму признаку равенства треугольников. Отсюда: AK = CP.
по второму признаку равенства треугольников. Отсюда: AK = CP.
При симметрии относительно прямой BM точки K и P переходят друг в друга, точка M — сама в себя. Следовательно, отрезки MP и MK перейдут друг на друга. Значит, MP = MK.
б) Из рассмотренной симметрии также следует: BH — ось симметрии  MH — ось симметрии
MH — ось симметрии  (H — точка пересечения BM и PK).
(H — точка пересечения BM и PK).
Пусть AB = BC = a,  В прямоугольном треугольнике ABM:
В прямоугольном треугольнике ABM: 

 Это с одной стороны. С другой стороны,
Это с одной стороны. С другой стороны,

Следовательно, 
По свойству биссектрисы внутреннего угла треугольника:  Если
Если  то
то 


 как два прямоугольных треугольника с общим острым углом.
как два прямоугольных треугольника с общим острым углом.
Коэффициент подобия 



Так как  то:
то:








Ответ: б) 15.
Примечание.
Это задание встречалась ранее в варианте 106 А. Ларина: см. задачу 562077.
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: б) 15.



