4. Тип Д15 C4 № 511275 
Сложная планиметрия. Многоугольники
i
В равнобокой описанной трапеции ABCD, где угол B тупой, а BC и AD — основания, проведены: 1) биссектриса угла B; 2) высота из вершины С; 3) прямая, параллельная AB и проходящая через середину отрезка CD.
а) Докажите, что все они пересекаются в одной точке.
б) Найдите расстояние между центрами вписанной и описанной окружностей трапеции ABCD, если известно, что BC = 8, AD = 18.
Решение. а) Задачу решим с максимально возможным привлечением метода координат. Поместим трапецию в декартову систему координат, как показано на рисунке.
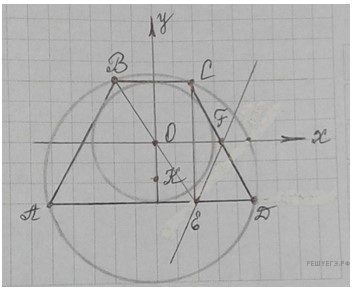
Пусть: r — радиус вписанной окружности;  — абсциссы вершин D и C соответственно,
— абсциссы вершин D и C соответственно,  — середина отрезка
— середина отрезка  Тогда:
Тогда:


Уравнение прямой 
Найдем угловой коэффициент  прямой АВ.
прямой АВ. 
Уравнение прямой, проходящей через точку F, параллельно прямой АВ, имеет вид:






Найдем точку пересечения этой прямой и прямой AD, для чего решим систему:







Таким образом, оказалось, что найденная прямая пересекает прямую AD в точке 
Так как центр вписанной окружности лежит на биссектрисе угла  то, зная координаты точек
то, зная координаты точек  и
и  можно получить уравнение биссектрисы.
можно получить уравнение биссектрисы.


Теперь найдем координаты пересечения прямых AD и 

Оказалось, что биссектриса угла  пересекает прямую AD в точке
пересекает прямую AD в точке 
Доказательство требуемого завершено.
б) Из условия получим:  По признаку окружности , вписанной в четырехугольник:
По признаку окружности , вписанной в четырехугольник:


Это — с одной стороны, с другой же стороны —  Значит,
Значит, 
Очевидно, центры обеих окружностей лежат на оси симметрии трапеции. Обозначим центр описанной окружности  Она лежит на пересечении серединного перпендикуляра к прямой
Она лежит на пересечении серединного перпендикуляра к прямой  и прямой
и прямой  Угловой коэффициент
Угловой коэффициент  прямой
прямой 

А угловой коэффициент  прямой, перпендикулярной CD, будет:
прямой, перпендикулярной CD, будет:

Уравнение прямой, проходящей через точку F с угловым коэффициентом  будет иметь вид:
будет иметь вид:  или
или 
Теперь найдем координаты точки K (точки пересечения оси симметрии трапеции и серединного перпендикуляра к отрезку BD).

Найденная ордината точки K и будет равна расстоянию между центрами двух окружностей.
Ответ: б) 
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: б)

511275
б)


воспользуемся геометрическим смыслом модуля. Левая ее часть на числовой прямой представляет собой сумму расстояний от точки
до точек (1) и (8) не больше 7. Следовательно, верно неравенство
Ясно, что
Докажем, что
Очевидно, что
Докажем, что
Действительно,
Получили очевидное неравенство.
будет выполнено неравенство
Действительно, уже при
имеем:
 PDF-версии:
PDF-версии: