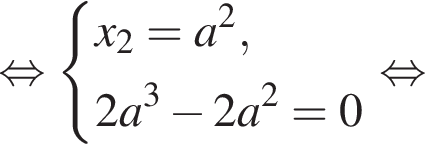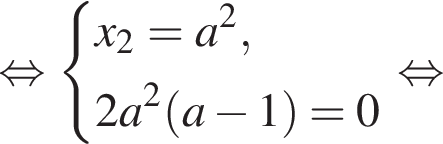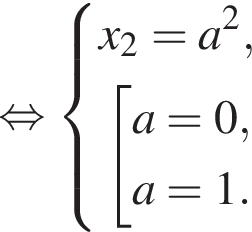1. Тип Д8 C1 № 511209 

Классификатор алгебры: Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Уравнения высших степеней
Методы алгебры: Формулы приведения
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
Дано уравнение 
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие промежутку 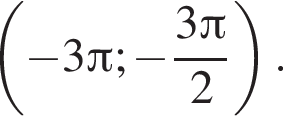
Решение. а) Последовательно получаем:



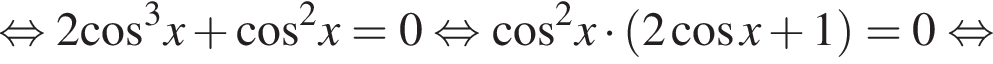



б) Отбор корней сделаем с помощью единичной окружности.



Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
511209
а)  б)
б) 
 б)
б) 
 где
где 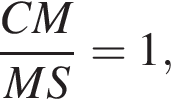 следовательно,
следовательно,  что и требовалось доказать.
что и требовалось доказать.

































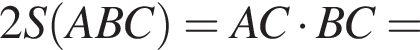














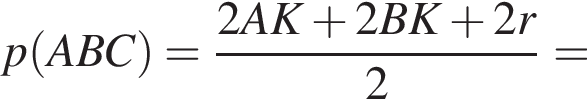





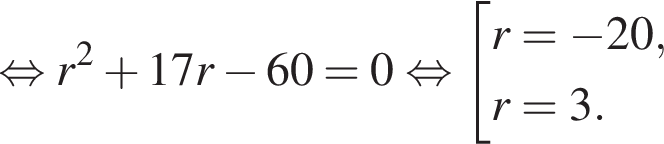
















 городских жителей и
городских жителей и 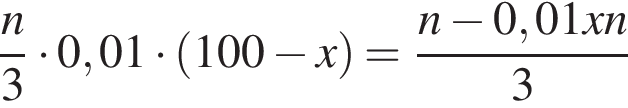 сельских жителей. Всего
сельских жителей. Всего 

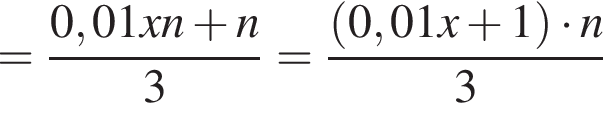


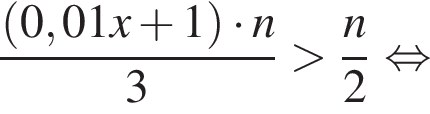
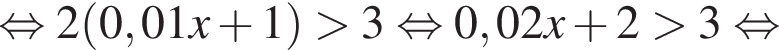






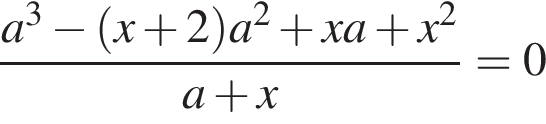



 * равен нулю и при этом
* равен нулю и при этом 




 Однако, это уравнение решений не имеет, значит, 0 не относится к числу искомых значений параметра.
Однако, это уравнение решений не имеет, значит, 0 не относится к числу искомых значений параметра. 
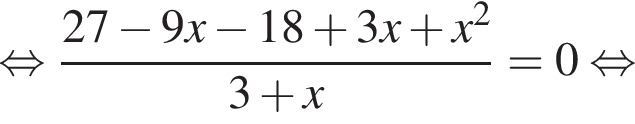

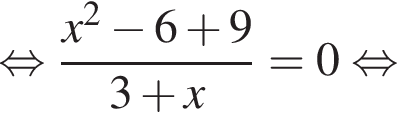


 удовлетворяют все значения а, за исключением 0 и 3. То есть уравнение (*) имеет два различных действительных корня при всех значениях а, отличных 0 и 3. Но нас интересует такое значение а, при котором один из корней упомянутого уравнения равен — a. Обозначим его x1. Другой же корень пусть будет x2, причем x1 ≠ x2. Тогда в соответствии с теоремой Виета:
удовлетворяют все значения а, за исключением 0 и 3. То есть уравнение (*) имеет два различных действительных корня при всех значениях а, отличных 0 и 3. Но нас интересует такое значение а, при котором один из корней упомянутого уравнения равен — a. Обозначим его x1. Другой же корень пусть будет x2, причем x1 ≠ x2. Тогда в соответствии с теоремой Виета: