7. Тип Д19 C7 № 508654 
Сложные задания на числа и их свойства. Числа и их свойства
i
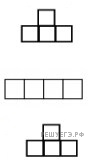 А) Можно ли клетчатую доску размером 12×12 полностью накрыть плитками, указанными на рисунке?
А) Можно ли клетчатую доску размером 12×12 полностью накрыть плитками, указанными на рисунке?
Б) Можно ли клетчатую доску размером 10×10 полностью накрыть плитками, указанными на рисунке?
В) Можно ли клетчатую доску размером 10×10 полностью накрыть плитками, указанными на рисунке?
(Плитки не должны накладываться друг на друга и выходить за край доски)
Решение. а) Да. Для этого достаточно показать, что квадрат 4 на 4 покрывается фигурками заданной
формы (это ясно). Доска же 12 на 12, в свою очередь, разбивается на квадраты 4 на 4.
б) Нет. Напишем в каждой клетке число 0 или 1 как изображено на рисунке 1. Сумма цифр на доске
равна 48. Каждая фигурка заданной формы содержит две единицы и два ноля. Соответственно
сумма цифр внутри каждой фигурки равна 2. Фигурок на доске должно быть 
таким образом, сумма всех цифр на доске должна получиться 50. А на самом деле она
равняется 48. Противоречие.
0 0 1 1 0 0 1 1 0 0
0 0 1 1 0 0 1 1 0 0
1 1 0 0 1 1 0 0 1 1
1 1 0 0 1 1 0 0 1 1
0 0 1 1 0 0 1 1 0 0
0 0 1 1 0 0 1 1 0 0
1 1 0 0 1 1 0 0 1 1
1 1 0 0 1 1 0 0 1 1
0 0 1 1 0 0 1 1 0 0
0 0 1 1 0 0 1 1 0 0
Рис. 1
в) Нет. Напишем в каждой клетке число 0 или 1 в шахматном порядке, как изображено на рисунке 2.
Сумма цифр на доске равна 50. Каждая фигурка заданной формы может содержать одну или
три единицы. Соответственно сумма цифр внутри каждой фигурки нечетная. Фигурок на
доске должно быть  таким образом, сумма всех цифр на доске будет нечетной. А
таким образом, сумма всех цифр на доске будет нечетной. А
она должна равняться 50. Противоречие.
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
Рис. 2
Ответ: а) да; б) нет; в) нет.
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Верно получены все перечисленные (см. критерий на 1 балл) результаты. | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующих результатов: — пример в п. а; — обоснованное решение п. б; — обоснование в п. в того, что S может принимать все целые значения (отличные от −1 и 1); — обоснование в п. в того, что равенства S = −1 и S = 1 невозможны. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |
Ответ: а) да; б) нет; в) нет.
508654
а) да; б) нет; в) нет.

тоже не подходит, так как
Докажем, что
несложно понять, искомых корней не будет.
Но
б)
 PDF-версии:
PDF-версии: