а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. а) Преобразуем 
Заданное уравнение будет равносильным уравнению 
Найдем ограничения на 
Из последнего неравенства следует, что ни при каких значениях x равенство 
невыполнимо. Следовательно, левая часть исходного уравнения обращается в нуль только при тех значениях x, при которых выполняется условие 
В общем случае уравнению 
удовлетворяют все числа типа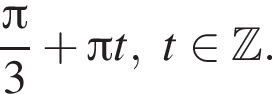 
Но с учетом ограничений на x получим, что 
б) При 
Но уже при 
корни уравнения выходят за пределы рассматриваемого отрезка. Дальнейшие поиски просто излишни.
Ответ: а) 
б) 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
б) б) 
имеет координаты {1; 1; 1} и потому плоскость имеет уравнение 
Поскольку она проходит через центр куба, координата которого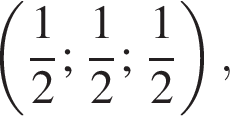 
получаем что 
Итак, уравнение этой плоскости имеет вид 
В частности, точки, координаты которых — в любом порядке — равны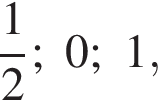 
лежат в этой плоскости. Нетрудно видеть, что эти шесть точек являются серединами ребер BC, CD, DD1, A1D1, A1B1, B1B. Если соединить эти точки, получится шестиугольник, все стороны которого имеют длину, равную половине длины диагонали грани куба, то есть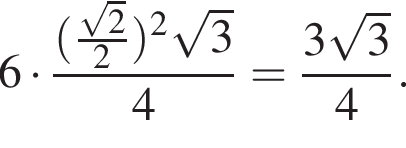 
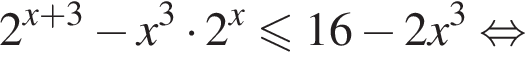
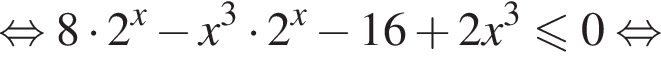
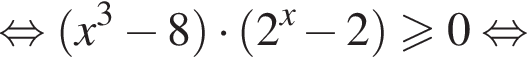
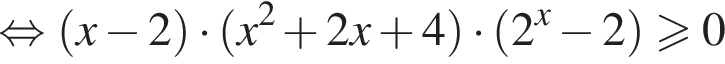
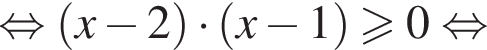
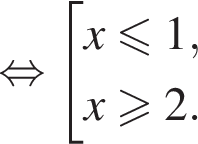
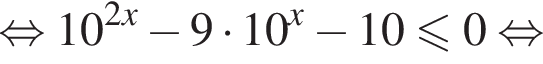
Кроме того, этому же числу равны все расстояния от центра куба до этих точек, поэтому сечение имеет форму правильного шестиугольника со стороной 
и площадь его равна: 
Следовательно, решением второго неравенства системы является множество 
(равные хорды стягивают равные дуги, углы опирающиеся на равные дуги, равны), откуда ABCD — равнобедренная трапеция. Ее высота равна 
Искомая окружность тогда — описанная окружность треугольника DAC. Найдем ее радиус по формуле
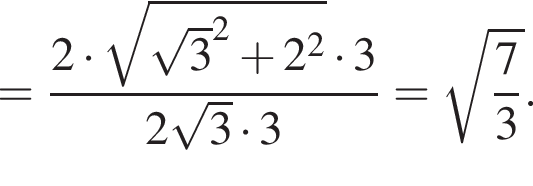
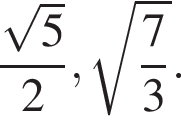
имеет хотя бы одно решение.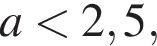
то можно выбрать 
и уравнение не будет иметь корней:
то при любом b можно выбрать 
Такое a подходит.
то можно выбрать 
и уравнение не будет иметь корней:
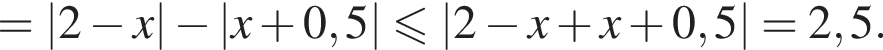
Пусть 
тогда есть минимум два способа уравновесить массу 
где r — это остаток от деления m на M. Значит, 
значит, 501 делится на M. Найдя M, можно определить массу второй по тяжести гирьки. Аналогичными рассуждениями получаем, что она должна быть делителем M. Разложим 501 на простые множители: 
Значит, существует всего два набора, кроме состоящего из одних однограммовых гирек. Первый набор состоит из двух гирек массой 167 граммов и 166 гирек массой по 1 грамму. Второй набор состоит из 166 гирек массой по 3 грамма и двух гирек массой по 1 грамму.