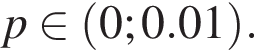1. Тип Д8 C1 № 505736 

Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Понижение порядка тригонометрического уравнения, Тригонометрические формулы суммы и разности функций, Формулы половинного аргумента
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. а) В левой части уравнения воспользуемся формулами понижения степени:















Заметим, что серия корней  содержится в серии
содержится в серии  Следовательно, решениями исходного уравнения являются числа вида
Следовательно, решениями исходного уравнения являются числа вида 
б) 




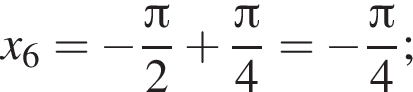

Ответ: а)  б)
б) ![]()
![]()
![]()
![]()

![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
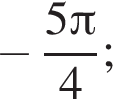




 б)
б) 
505736
а)  б)
б) 
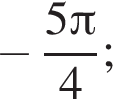




 б)
б) 
 Проведем в гранях ABS и ADS отрезки EK и FM, параллельные
Проведем в гранях ABS и ADS отрезки EK и FM, параллельные  Докажем, что она лежит в плоскости сечения. Тогда искомое сечение - пятиугольник
Докажем, что она лежит в плоскости сечения. Тогда искомое сечение - пятиугольник 
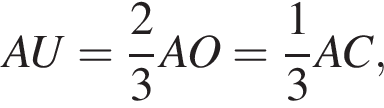 откуда треугольники ASC и UTC подобны (по двум сторонам) и, значит,
откуда треугольники ASC и UTC подобны (по двум сторонам) и, значит,  откуда и следует нужное утверждение. (AU действительно медиана, поскольку
откуда и следует нужное утверждение. (AU действительно медиана, поскольку  ), то есть AU составляет со стороной такой же угол, какой в подобном треугольнике составляет медиана.)
), то есть AU составляет со стороной такой же угол, какой в подобном треугольнике составляет медиана.) Отметим середину SC -- точку
Отметим середину SC -- точку 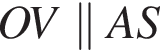 как средняя линия. Заметим, что треугольник SCD равносторонний, поэтому
как средняя линия. Заметим, что треугольник SCD равносторонний, поэтому 
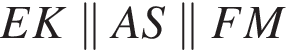 и
и  Найдем его угол.
Найдем его угол.









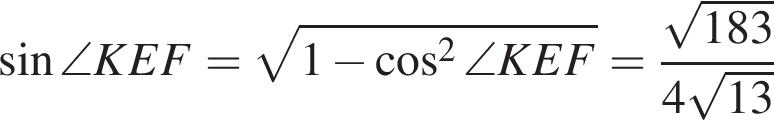


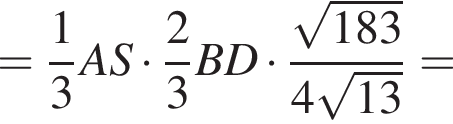











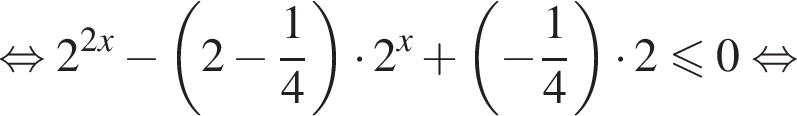










 Для таких значений x будем иметь:
Для таких значений x будем иметь:


 на множестве
на множестве  Очевидно, искомыми значениями переменной будут элементы множества
Очевидно, искомыми значениями переменной будут элементы множества  Ясно, что пересечением решений обоих неравенств системы будет множество
Ясно, что пересечением решений обоих неравенств системы будет множество 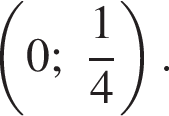
 что и требовалось доказать.
что и требовалось доказать.









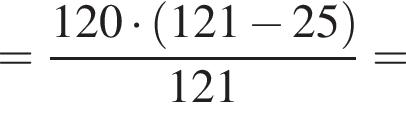

 Откуда:
Откуда:



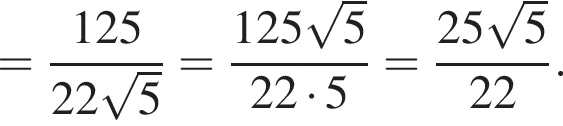

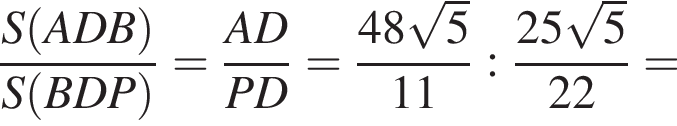


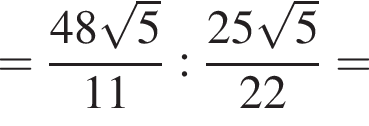


 то:
то:




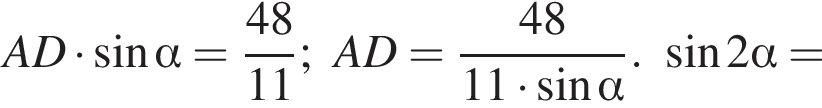











 выполняется хотя бы для одного числа x такого, что | x | < 0,01.
выполняется хотя бы для одного числа x такого, что | x | < 0,01. то подходит
то подходит  так как
так как 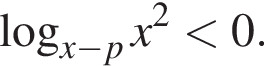

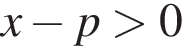 )
)


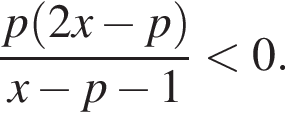
 Решая неравенство методом интервалов, получим
Решая неравенство методом интервалов, получим 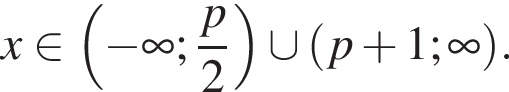 Учитывая ОДЗ, получим
Учитывая ОДЗ, получим 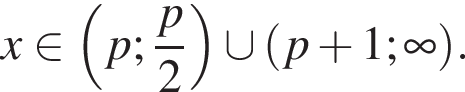

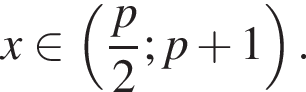 Учитывая ОДЗ, получим
Учитывая ОДЗ, получим  Нужные точки найдутся в этом множестве если
Нужные точки найдутся в этом множестве если