1. Тип Д8 C1 № 521692 
Методы алгебры: Введение замены, Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
Решение. а) Обозначив 
получим 
откуда 
или 
Второй вариант невозможен.
Первый дает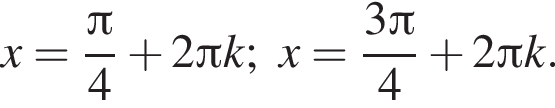 
б) На указанном промежутке лежит 
Ответ: а)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а) б)
б) 521692
а) б)
б) Методы алгебры: Введение замены, Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
а высота СС1 равна 7,5. На ребре B1C1 отмечена точка Р так, что B1P:PC1 = 1 : 3. Точки Q и М являются серединами сторон АВ и A1C1 соответственно. Плоскость α параллельна прямой АС и проходит через точки Р и Q.
Пусть 
— середина ребра 
Тогда 
— проекция BM на плоскость основани. Она перпендикулярна средней линии QT основания, поэтому и 
такая, что 
Тогда 
и Значит, BN — проекция BM на плоскость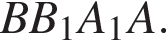 
Если мы докажем, что 
то и 
и тогда 
поэтому AQSN — параллелограмм и 
Осталось проверить, что треугольник BNA — прямоугольный. 
Опустим перпендикуляр из M на прямую 
Поскольку он лежит в плоскости 
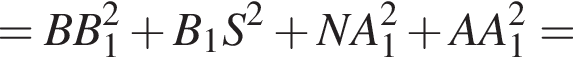
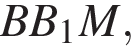он будет заодно перпендикулрен и прямой QT, Значит, он-то и есть искомое расстояние. Вычислим теперь его длину через площадь треугольника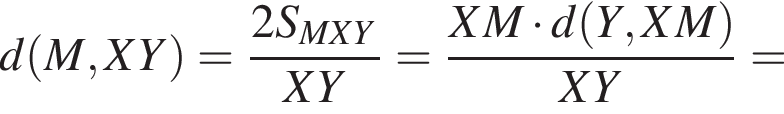 
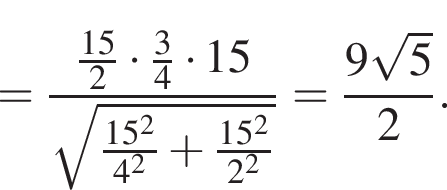
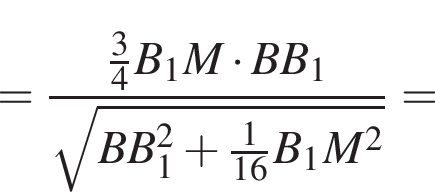
Ясно, что 
При таких x получим по методу рационализации
отсекающая от прямой ВС отрезок 
и касающаяся прямой АС в точке А. Из точки В проведен перпендикуляр к прямой ВС до пересечения с прямой АС в точке F.
длина диаметра окружности также равна 
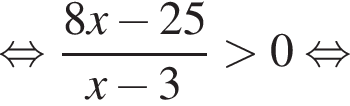
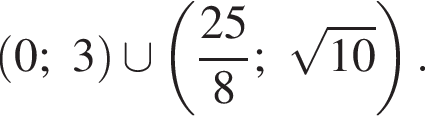
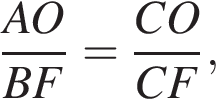откуда
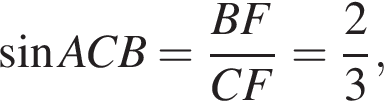
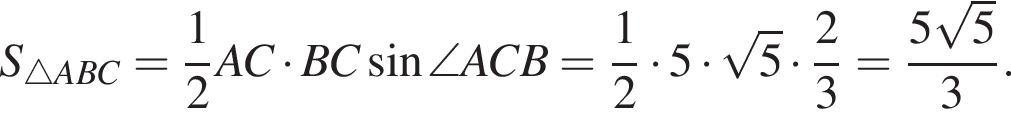
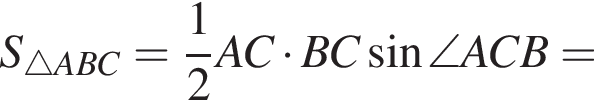
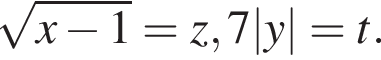Тогда каждому неотрицательному решению системы
и они не равны нулю, то можно еще поменять местами z и t и получить 8 решений.
либо они равны друг другу (и тогда равны 
) и 
Осталось убедиться, что в этих случаях других неотрицательных решений система не имеет.
имеем
и 
дающие по два решения системы. Других нет, поскольку возводя первое уравнение в четвертую степень и вычитая второе, находим 
что для неотрицательных чисел возможно только при 
имеем
дающее четыре решения системы. Других нет, поскольку выразив из первого уравнения z и подставив во второе, получим
а вторая корней не имеет.
то вычисленная во второй раз разность отличается от первой дополнительным слагаемым
и 
поэтому
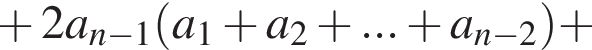
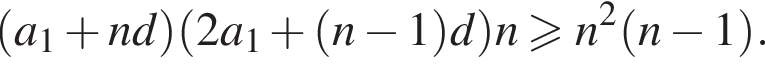
Значит, 13 членов в начальной прогрессии быть не может. 
следует, что n является делителем числа 1768 = 2 · 2 · 2 · 13 · 17. Наибольший делитель, меньший 13, равен 8. При n = 8 получаем
то левая часть не меньше, чем 
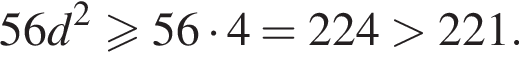Следовательно, d = 1. Получаем уравнение