Ре­ше­ние. 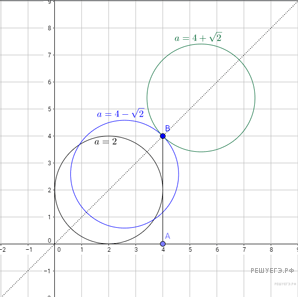а)  По­сле­до­ва­тель­но по­лу­ча­ем:

б)  Отбор кор­ней про­из­ве­дем с по­мо­щью еди­нич­ной окруж­но­сти.

Ответ: а) б)

Ре­ше­ние.

А)  Стро­им по­сле­до­ва­тель­но:

1.  От­ре­зок ВК.

2.  От­ре­зок KF, F ∈ PD, KF || DC.

3.  От­ре­зок AF. AFKB  — ис­ко­мое се­че­ние.

По­ло­же­ние точек А, В и К за­да­но усло­ви­ем за­да­чи. Нам сле­ду­ет до­ка­зать:

1)  F ∈ (ABK); 2) AFKB  — тра­пе­ция. До­ка­жем.

1)  Из усло­вия: DC || AB, по по­стро­е­нию: KF || DC. Сле­до­ва­тель­но, KF || AB по свой­ству тран­зи­тив­но­сти от­но­ше­ния па­рал­лель­но­сти. Так как через две па­рал­лель­ные пря­мые можно про­ве­сти толь­ко одну плос­кость, то F ∈ (ABK).

2)  Для до­ка­за­тель­ства того, что AFKB  — тра­пе­ция, до­ста­точ­но убе­дить­ся, что AF и KB не па­рал­лель­ны. Пред­по­ло­жим, что AF || KB, тогда AFKB  — па­рал­ле­ло­грамм, от­ку­да: FK = AB, сле­до­ва­тель­но, FK = CD, чего быть не может, так как по смыс­лу за­да­чи FK < CD. Зна­чит, пред­по­ло­же­ние AF || KB не­вер­но.

Б)  Гео­мет­ри­че­ский спо­соб ре­ше­ния.

Для опре­де­лен­но­сти при­мем 4 за длину ребер пи­ра­ми­ды. Пусть О  — точка пе­ре­се­че­ния диа­го­на­лей ос­но­ва­ния, Q  — се­ре­ди­на CD, H  — се­ре­ди­на АВ, Е  — се­ре­ди­на KF, М  — точка пе­ре­се­че­ния РО и E, тогда:

В по тео­ре­ме Ме­не­лая: Итак, PM = 6OM. А это зна­чит, что

До­ка­жем, что ис­ко­мый угол.

AB пря­мая, по ко­то­рой пе­ре­се­ка­ют­ся плос­ко­сти АВК и АВС, PO ⊥ (ABC), M  — на­клон­ная, O  — про­ек­ция на­клон­ной. O ⊥ AB, сле­до­ва­тель­но, MH ⊥ AB.

Ко­ор­ди­нат­но-век­тор­ный спо­соб ре­ше­ния.

По­ме­стим за­дан­ную пи­ра­ми­ду в де­кар­то­ву си­сте­му ко­ор­ди­нат, как по­ка­за­но на ри­сун­ке. Для опре­де­лен­но­сти при­мем за длину ребер пи­ра­ми­ды 4. Пусть О  — точка пе­ре­се­че­ния диа­го­на­лей ос­но­ва­ния пи­ра­ми­ды, Q  — се­ре­ди­на CD, F  — се­ре­ди­на АВ, Е  — се­ре­ди­на KF, М  — точка пе­ре­се­че­ния РО и F, тогда : ап­пли­ка­та точки К будет равна т. е.

Най­дем ко­ор­ди­на­ты нуж­ных точек:

Будем ис­кать урав­не­ние плос­ко­сти АВК при d = 2, для чего будем ре­шать си­сте­му урав­не­ний:

      Итак, урав­не­ние плос­ко­сти АВК имеет вид: или Нор­маль­ный век­тор этой плос­ко­сти

Урав­не­ние плос­ко­сти ос­но­ва­ния пи­ра­ми­ды: z = 0, нор­маль­ный век­тор ко­то­рой Ис­ко­мый угол  — угол между век­то­ра­ми и

Ответ: Б)

Ре­ше­ние. Пусть тогда: Най­дем корни чис­ли­те­ля левой части по­след­не­го не­ра­вен­ства.

Не­ра­вен­ство решим ме­то­дом ин­тер­ва­лов.

Ин­тер­ва­лы
Знак вы­ра­же­ния	−	+	−	+

Итак, Пе­рей­дем к пе­ре­мен­ной х.    (*)

Най­дем корни чис­ли­те­ля левой части по­след­не­го не­ра­вен­ства:

Далее имеем:

Решим по­след­нее не­ра­вен­ство ме­то­дом ин­тер­ва­лов.

За­ме­тим, что

Ин­тер­ва­лы
Знак вы­ра­же­ния	+	+	−	+	−	+

Ре­ше­ния не­ра­вен­ства (**) :

Объ­еди­нив ре­ше­ния не­ра­венств (*) и (**) будем иметь:

Ответ:

Ре­ше­ние.

А)  Из­вест­но, что BP · AP = DP · CP.

Δ APD ~ Δ CPB, так как у них ∠ P  — общий, ∠ ABC = ∠ ADP как впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же дугу АС. От­сю­да: или AD · BP = BC · DP, что и тре­бо­ва­лось до­ка­зать.

Б)  Δ APC ~ Δ DPB с не­ко­то­рым ко­эф­фи­ци­ен­том по­до­бия k, так как ∠ P  — общий, Сле­до­ва­тель­но,

А это зна­чит, что т. е.

Ответ: б) 12.

Ре­ше­ние. Пусть из каж­до­го со­су­да от­ли­ли х л жид­ко­сти. При­чем:

Со­бы­тия и факты		Пер­вый сосуд	Вто­рой сосуд
1	Пер­во­на­чаль­ный объем рас­тво­ра (л)	21	9
	В том числе объем чи­стой кис­ло­ты (л)
2	От­ли­ли жид­ко­сти (л)	x	x
	В том числе чи­стой кис­ло­ты (л)	0,75	0,3
3	Оста­лось рас­тво­ра (л)	21 − x	9 − x
	В том числе чи­стой кис­ло­ты (л)	15,75 – 0,75x	2,7 – 0,3х
4	Вы­ли­ли в со­су­ды кис­ло­ты дру­гой кон­цен­тра­ции, чем было пер­во­на­чаль­но (л)	x	x
	В том числе чи­стой кис­ло­ты (л)	0,3	0,75
5	Стало рас­тво­ра (л)	21 − x + x = 21	9 − x + x = 9
	В том числе чи­стой кис­ло­ты (л)	15,75 – 0,75х+ 0,3х = 15,75 – 0,45х	2,7 – 0,3х + 0,75х = 2,7 + 0,45х
6	Кон­цен­тра­ция по­лу­чен­но­го рас­тво­ра (%)

Со­глас­но усло­вию за­да­чи:

Ответ: 6,3 л.

Ре­ше­ние. Пер­вое урав­не­ние си­сте­мы задаёт мно­же­ство точек (x; y), сумма рас­сто­я­ний от ко­то­рых до точек с ко­ор­ди­на­та­ми A(4; 0) и B(4; 4) равна 4. Так как рас­сто­я­ние между ука­зан­ны­ми точ­ка­ми в точ­но­сти 4, то это урав­не­ние задаёт от­ре­зок AB.

Вто­рое урав­не­ние си­сте­мы задаёт окруж­ность ра­ди­у­са 2, центр ко­то­рой (a; a) лежит на пря­мой y = x. При уве­ли­че­нии a окруж­ность пе­ре­ме­ща­ет­ся впра­во-вверх вдоль этой пря­мой.

При a < 2 окруж­ность лежит левее от­рез­ка и не имеет с ним общих точек. Зна­чит, си­сте­ма не имеет ре­ше­ний.

При a = 2 окруж­ность ка­са­ет­ся от­рез­ка и, сле­до­ва­тель­но, имеет с ним одну общую точку.

Найдём зна­че­ния па­ра­мет­ра a, при ко­то­рых точка B лежит на рас­смат­ри­ва­е­мой окруж­но­сти, под­ста­вив её ко­ор­ди­на­ты в урав­не­ние окруж­но­сти:

Ясно, что при мень­шем из этих зна­че­ний B лежит на верх­ней по­лу­окруж­но­сти, а при боль­шем  — на ниж­ней.

Таким об­ра­зом, при си­сте­ма имеет два ре­ше­ния, при си­сте­ма имеет одно ре­ше­ние, при си­сте­ма не имеет ре­ше­ний.

Ответ:

При­ведём дру­гое ре­ше­ние.

Пер­вое урав­не­ние си­сте­мы за­да­ет мно­же­ство точек плос­ко­сти (х; у) сумма рас­сто­я­ний от ко­то­рых до точек (4; 0), (4; 4), ле­жа­щих на пря­мой x = 4, равна 4. Сле­до­ва­тель­но, это урав­не­ние фак­ти­че­ски за­да­ет от­ре­зок [0; 4], ле­жа­щий на пря­мой x = 4. Этот же от­ре­зок можно за­дать си­сте­мой:

Тре­бу­ет­ся найти все зна­че­ния па­ра­мет­ра а, при каж­дом из ко­то­рых си­сте­ма имеет ровно одно ре­ше­ние.

Под­ста­вим зна­че­ние x = 4 в тре­тье усло­вие по­след­ней си­сте­мы. По­лу­чим:

      (*)

Далее най­дем зна­че­ния а, при ко­то­рых по­след­нее урав­не­ние на [0; 4] имеет ровно один ко­рень.

Нас устро­ят сле­ду­ю­щие си­ту­а­ции (см. также ри­су­нок):

1)  Урав­не­ние имеет два корня, один из ко­то­рых при­над­ле­жит ин­тер­ва­лу (0; 4), дру­гой лежит вне от­рез­ка [0; 4].

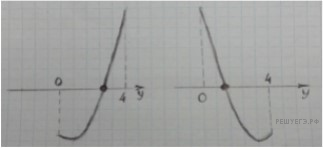
2)  Урав­не­ние имеет два корня, один из ко­то­рых равен 0 или 4, дру­гой лежит вне от­рез­ка [0; 4].

3)  Урав­не­ние имеет един­ствен­ный ко­рень, ко­то­рый при­над­ле­жит ин­тер­ва­лу (0; 4).

Рас­смот­рим функ­цию

Пер­вая си­ту­а­ция воз­мож­на тогда и толь­ко тогда, когда будет вы­пол­не­но не­ра­вен­ство: До­ка­жем это.

Пусть урав­не­ние (*) имеет два раз­лич­ных корня и при­чем Функ­ция ме­ня­ет знак толь­ко в точ­ках и Но от­рез­ку [0; 4] при­над­ле­жит толь­ко точка ко­то­рая яв­ля­ет­ся внут­рен­ней точ­кой этого от­рез­ка, сле­до­ва­тель­но, на кон­цах от­рез­ка знаки функ­ции обя­за­ны быть раз­ны­ми. Не­об­хо­ди­мость до­ка­за­на.

До­ка­жем до­ста­точ­ность. Пусть вы­пол­ня­ет­ся не­ра­вен­ство при любом зна­че­нии так как А это зна­чит, что ни при каком зна­че­нии а не может быть вы­пол­не­но ра­вен­ство

Не­ра­вен­ство сви­де­тель­ству­ет о су­ще­ство­ва­нии двух раз­лич­ных кор­ней у урав­не­ния (*). При­чем лишь один из них обя­за­тель­но лежит на ин­тер­ва­ле (0; 4). Если это было бы не так, то зна­че­ния функ­ций в точ­ках 0 и 4 имели бы оди­на­ко­вый знак. Кроме того, вто­рой ко­рень не может сов­па­дать с 4 (сов­па­де­ние с 0, как по­ка­за­но выше, во­об­ще не­воз­мож­но), так как в про­тив­ном слу­чае было бы вер­ным ра­вен­ство

Итак, решим не­ра­вен­ство

Рас­смот­рим вто­рую си­ту­а­цию.

Пусть y = 4. Тогда:

Вы­чис­лим зна­че­ние у при каж­дом из по­лу­чен­ных зна­че­ний а.

Если то

За­ме­тим, что оба корня при­над­ле­жат от­рез­ку [0; 4]. Сле­до­ва­тель­но, зна­че­ние ис­ко­мым не яв­ля­ет­ся.

Если же то

Но

При зна­че­нии рас­смат­ри­ва­е­мое урав­не­ние на [0; 4] имеет ровно один ко­рень, зна­чит, сле­ду­ет от­не­сти к числу ис­ко­мых.

Те­перь рас­смот­рим тре­тью си­ту­а­цию. По­тре­бу­ем, чтобы чет­верть дис­кри­ми­нан­та урав­не­ния (*) была равна нулю.

При

При

Сле­до­ва­тель­но, при дан­ной си­ту­а­ции ис­ко­мое зна­че­ние а равно 2.

Объ­еди­нив по­лу­чен­ные ре­зуль­та­ты, будем иметь:

Ответ:

Ре­ше­ние. Пусть ос­но­ва­ния тра­пе­ции равны a и b, b > a. Вве­дем обо­зна­че­ния, как по­ка­за­но на ри­сун­ках. Для еди­но­об­ра­зия за­пи­сей в каж­дом из слу­ча­ев обо­зна­чим ис­ко­мый от­ре­зок EF и прием его длину за х.

1. От­ре­зок, про­хо­дя­щий через точку пе­ре­се­че­ния диа­го­на­лей. До­стро­им тра­пе­цию до па­рал­ле­ло­грам­ма, как по­ка­за­но на ри­сун­ке. Тре­уголь­ни­ки BOC и AOD по­доб­ны, их вы­со­ты от­но­сят­ся как Тре­уголь­ни­ки FCG также FDH по­доб­ны, их вы­со­ты от­но­сят­ся как По­сколь­ку ука­зан­ные пары тре­уголь­ни­ков имеют рав­ные вы­со­ты, по­лу­ча­ем: от­ку­да

От­ме­тим, что най­ден­ная длина от­рез­ка яв­ля­ет­ся сред­ним гар­мо­ни­че­ским ос­но­ва­ний.

2. По­доб­ные тра­пе­ции. Если тра­пе­ции ALFD и LBCF по­доб­ны, то От­сю­да

От­ме­тим, что най­ден­ная длина от­рез­ка яв­ля­ет­ся сред­ним гео­мет­ри­че­ским ос­но­ва­ний.

3. Сред­няя линия тра­пе­ции. Тре­уголь­ник BCF равен тре­уголь­ни­ку FDG по сто­ро­не и двум при­ле­жа­щим к ней углам. Из ра­вен­ства сле­ду­ет, что BF  =  FG , по­это­му EF  — сред­няя линия тре­уголь­ни­ка ABG, а тогда EF || AG,

От­ме­тим, что най­ден­ная длина от­рез­ка яв­ля­ет­ся сред­ним ариф­ме­ти­че­ским ос­но­ва­ний.

4. Рав­но­ве­ли­кие тра­пе­ции. До­стро­им тра­пе­цию до тре­уголь­ни­ка, как по­ка­за­но на ри­сун­ке. В силу по­до­бия тре­уголь­ни­ков PBC, PEF и PAD имеем:

Скла­ды­вая ра­вен­ства, по­лу­ча­ем от­ку­да

От­ме­тим, что най­ден­ная длина от­рез­ка яв­ля­ет­ся сред­ним квад­ра­тич­ным ос­но­ва­ний.

Не­ра­вен­ства между сред­ни­ми. Из­вест­но, что для по­ло­жи­тель­ных чисел a и b их сред­нее гар­мо­ни­че­ское не боль­ше сред­не­го гео­мет­ри­че­ско­го, сред­нее гео­мет­ри­че­ское не боль­ше сред­не­го ариф­ме­ти­че­ско­го, а сред­нее ариф­ме­ти­че­ское не боль­ше сред­не­го квад­ра­тич­но­го; при­чем ра­вен­ства до­сти­га­ют­ся толь­ко в слу­чае ра­вен­ства чисел a и b:

Ил­лю­стра­ция этих со­от­но­ше­ний пред­став­ле­на на ри­сун­ке.

До­ка­жем не­ра­вен­ства, по­пар­но воз­во­дя их в квад­рат: