1. Тип 13 № 648010 

Классификатор алгебры: Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы приведения
Уравнения. Тригонометрические уравнения, разложение на множители
i
а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 
Решение. а) Преобразуем уравнение:



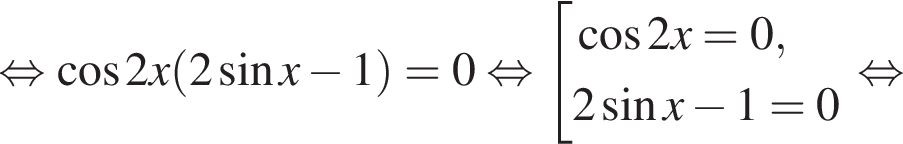




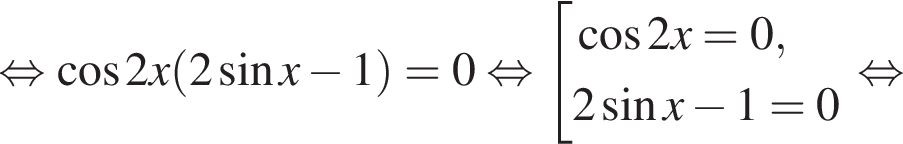





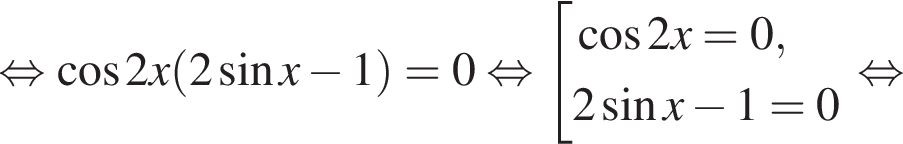














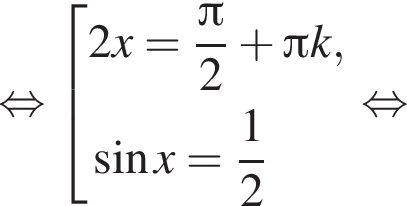

б) Отберем корни при помощи единичной окружности. Получаем: ![]()
![]()
![]()
![]()
Ответ: а)  б)
б) ![]()
![]()
![]()
![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
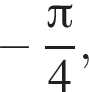

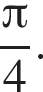
 б)
б) 648010
а)  б)
б) 
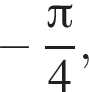

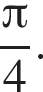
 б)
б) Классификатор алгебры: Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы приведения

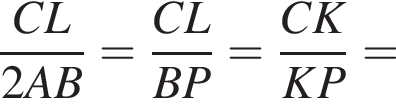



















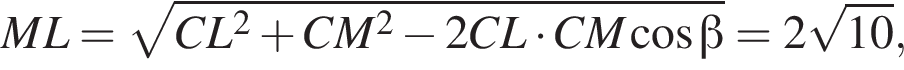


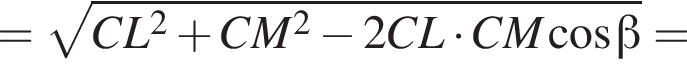
















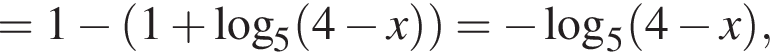
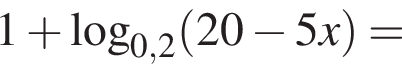






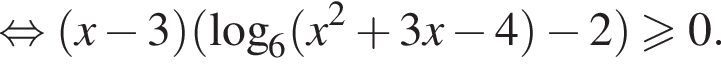
 и
и  совпадают, а потому исходное неравенство равносильно следующим:
совпадают, а потому исходное неравенство равносильно следующим:







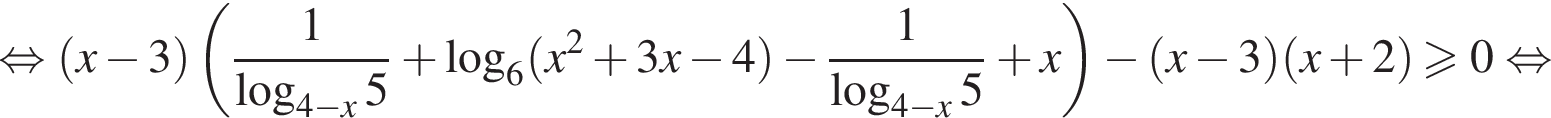






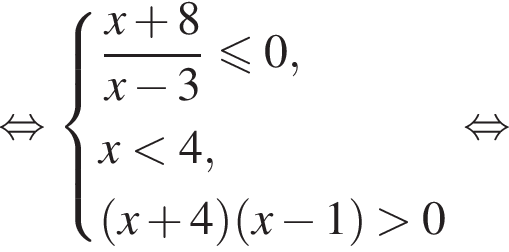

 тыс. рублей. Сравним числа ak и
тыс. рублей. Сравним числа ak и 



 имеет корни
имеет корни  или
или  Таким образом,
Таким образом,  при
при  при
при 

 угол A равен 60°. Точка D — точка пересечения биссектрис, точка Н — точка пересечения высот.
угол A равен 60°. Точка D — точка пересечения биссектрис, точка Н — точка пересечения высот.






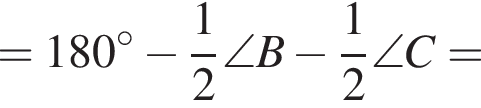
 следовательно, точки B, H, D, C лежат на одной окружности.
следовательно, точки B, H, D, C лежат на одной окружности. тогда
тогда  Значит,
Значит, 





 откуда
откуда 






 Тогда
Тогда




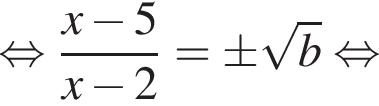
 или
или 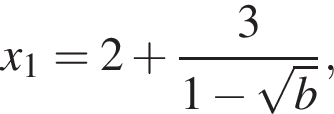
 Чтобы уравнение имело ровно два различных корня, больших чем 3, необходимо и достаточно, чтобы при
Чтобы уравнение имело ровно два различных корня, больших чем 3, необходимо и достаточно, чтобы при 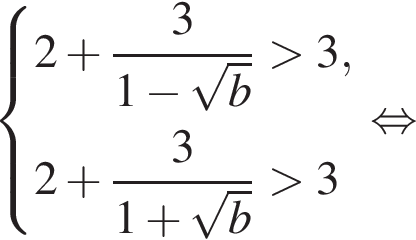
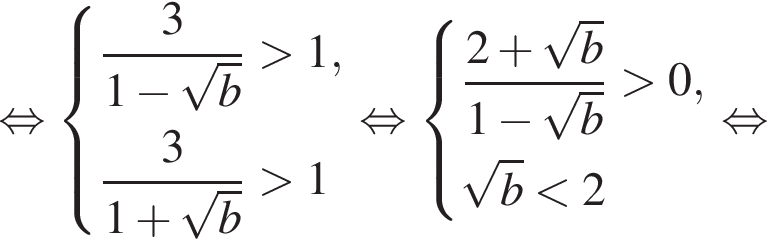













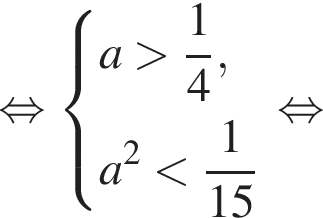







 откуда
откуда  то есть Петя сыграл 20 партий. В остальных
то есть Петя сыграл 20 партий. В остальных  партиях он не играл, значит, их сыграли Саша с Пашей.
партиях он не играл, значит, их сыграли Саша с Пашей.