Ре­ше­ние. а)   Решим урав­не­ние:

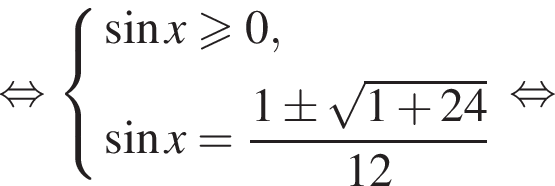
б)  

За­ме­ча­ние.

Во вклю­че­нии в си­сте­му усло­вия на­доб­но­сти нет, так как в про­цес­се ре­ше­ния усло­вие (пра­вой части вто­ро­го урав­не­ния) уже обес­пе­чит не­от­ри­ца­тель­ность левой части этого же урав­не­ния.

Ответ: а) б)

Ре­ше­ние. Пусть   — се­ре­ди­ны этих ребер со­от­вет­ствен­но. Тогда центр впи­сан­ной сферы лежит в би­сек­траль­ной плос­ко­сти, про­хо­дя­щей через ребро BD, то есть в (она пер­пен­ди­ку­дяр­на AC, по­это­му тет­ра­эдр сим­мет­ри­чен от­но­си­тель­но нее). Ана­ло­гич­но центр лежит и в то есть лежит на от­рез­ке Оче­вид­но (по­сколь­ку лежит в плос­ко­стях, пер­пен­ди­ку­ляр­ных этим от­рез­кам). Тогда

Тогда

Далее,

Най­дем ра­ди­ус впи­сан­ной сферы. Он равен

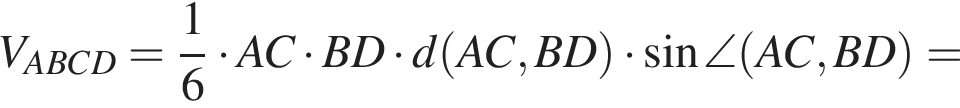
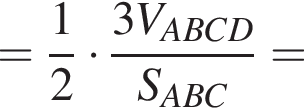
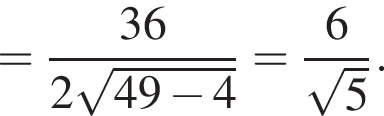
Итак, на от­рез­ке рас­по­ла­га­ет­ся точка на рас­сто­я­нии от плос­ко­сти ABC, при этом рас­сто­я­ния от точек и равны и Зна­чит, она делит этот от­ре­зок в от­но­ше­нии и рас­по­ла­га­ет­ся на рас­сто­я­нии от точки Это и есть ответ.

Ответ:

Ре­ше­ние. Решим пер­вое не­ра­вен­ство си­сте­мы. Най­дем огра­ни­че­ния на х: Для таких

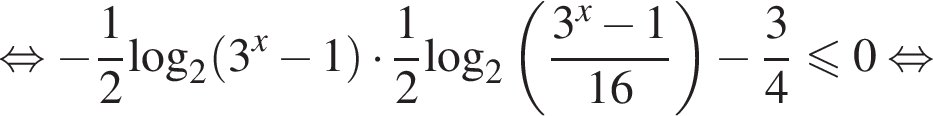
Пусть Тогда:

Таким об­ра­зом,

Ре­ше­ния пер­во­го не­ра­вен­ства си­сте­мы с уче­том огра­ни­че­ний на

Те­перь рас­смот­рим вто­рое не­ра­вен­ство си­сте­мы на мно­же­стве ре­ше­ний пер­во­го не­ра­вен­ства.

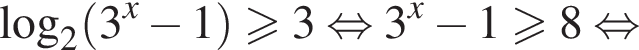
Не­труд­но за­ме­тить, что при вы­ра­же­ние смыс­ла не имеет, по­сколь­ку при этих зна­че­ни­ях x

При вто­рое не­ра­вен­ство си­сте­мы при­мет вид:

Но по­лу­чен­ное не­ра­вен­ство ре­ше­ний не имеет, по­сколь­ку Таким об­ра­зом, ни одно ре­ше­ние пер­во­го не­ра­вен­ства не яв­ля­ет­ся также ре­ше­ни­ем вто­ро­го не­ра­вен­ства.

Ответ: ре­ше­ний нет.

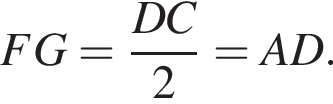Ре­ше­ние. а)  Обо­зна­чим се­ре­ди­ны от­рез­ков BA, BD, BC за E, F, G со­от­вет­ствен­но. Тогда EG  — сред­няя линия тре­уголь­ни­ка ABC, и точка F лежит на ней. По­сколь­ку FG  — сред­няя линия DBC, то Итак, в че­ты­рех­уголь­ни­ке AFGD две сто­ро­ны равны и па­рал­лель­ны, зна­чит, он па­рал­ле­ло­грамм и

б)  По тео­ре­ме ко­си­ну­сов в тре­уголь­ни­ке ABC имеем от­ку­да

По тео­ре­ме ко­си­ну­сов в тре­уголь­ни­ке DGC имеем от­ку­да

Ответ:

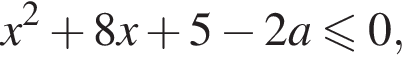Ре­ше­ние. При имеем то есть Если это во­об­ще не­воз­мож­но. Кроме того, при имеем и воз­рас­та­ет при по­это­му на дан­ном про­ме­жут­ке нет ре­ше­ний не­ра­вен­ства.

Если же то все воз­мож­ные целые x на­хо­дят­ся в про­ме­жут­ке по­сколь­ку Мы го­во­рим лишь о воз­мож­но­сти, по­сколь­ку не срав­ни­ва­ли эти зна­че­ния с гра­ни­ца­ми про­ме­жут­ка. Не­со­мнен­но, при не­ко­то­рых a эти точки так и не по­па­дут на нуж­ные про­ме­жут­ки.

При имеем то есть Если это во­об­ще не­воз­мож­но. Кроме того, при имеем и убы­ва­ет при по­это­му на дан­ном про­ме­жут­ке нет ре­ше­ний не­ра­вен­ства.

Если же то все воз­мож­ные целые x на­хо­дят­ся в про­ме­жут­ке 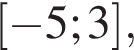по­сколь­ку

Итак, толь­ко целые числа от −7 до 3 воз­мож­но могут хоть при каких-то a (от −5,5 до 1 ) быть ре­ше­ни­я­ми дан­но­го не­ра­вен­ства. Вы­яс­ним те­перь про каж­дое из них, при каких a оно дей­стви­тель­но ре­ше­ние.

Оче­вид­но, это не­воз­мож­но при до­пу­сти­мых a.

Оче­вид­но, это не­воз­мож­но при до­пу­сти­мых a.

Оче­вид­но, это воз­мож­но толь­ко при

Решая это не­ра­вен­ство, на­хо­дим

Решая это не­ра­вен­ство, на­хо­дим

Решая это не­ра­вен­ство, на­хо­дим

Оче­вид­но, это воз­мож­но толь­ко при

Оче­вид­но, это не­воз­мож­но при по­ло­жи­тель­ных a, а при про­чих a имеем что тоже не­воз­мож­но.

Оче­вид­но, это не­воз­мож­но при до­пу­сти­мых a.

Оче­вид­но, это не­воз­мож­но при до­пу­сти­мых a.

Оче­вид­но, это не­воз­мож­но при до­пу­сти­мых a.

Из этой таб­ли­цы видно, что ни при каком a не будет более трех целых ре­ше­ний. Ровно три ре­ше­ния по­лу­ча­ют­ся при или

Ответ:

Ре­ше­ние. а)  В конце у всех гно­мов ока­за­лось по пол­лит­ра мо­ло­ка. Зна­чит, перед по­след­ним пе­ре­ли­ва­ни­ем у четвёртого гнома было 4/3 · 1/2 = 2/3 л, у пер­во­го 1/2 – 1/6 = 1/3 л, а у двух осталь­ных  — по пол­лит­ра. Ана­ло­гич­но, перед тр­тьим пе­ре­ли­ва­ни­ем у тре­тье­го гнома было 2/3 л, у четвёртого 2/3 – 1/6 = 1/2 л, у вто­ро­го  — тоже пол­лит­ра, а у пер­во­го  — 1/3 л. Со­от­вет­ствен­но, перед вто­рым пе­ре­ли­ва­ни­ем у вто­ро­го гнома было 2/3 л, у тре­тье­го и четвёртого  — по пол­лит­ра, а у пер­во­го  — 1/3 л. На­ко­нец, в на­ча­ле у 1-го было 4/9 л, у вто­ро­го 5/9 л, у тре­тье­го и четвёртого  — по пол­лит­ра.

б)  Раз в конце у всех гно­мов ока­за­лось мо­ло­ка столь­ко, сколь­ко было в на­ча­ле, то каж­дый отдал столь­ко же мо­ло­ка, сколь­ко по­лу­чил. Если у 1-го гнома было 4 части мо­ло­ка, то он пе­ре­лил вто­ро­му одну часть, ко­то­рая долж­на со­ста­вить чет­верть его мо­ло­ка после пе­ре­ли­ва­ния (чтобы он мог от­лить одну часть тре­тье­му). То есть у вто­ро­го было 3 части. Ана­ло­гич­но, у тре­тье­го и четвёртого было по 3 части. Зна­чит, от­но­ше­ние объ­е­ма мо­ло­ка у гно­мов было 4 : 3 : 3 : 3. Ре­ша­ем урав­не­ние по­лу­ча­ем: 4x + 3x + 3x + 3x + = 2,

Ответ: а) у пер­во­го гнома было 4/9 л, у вто­ро­го  — 5/9 л, у тре­тье­го и четвёртого  — по пол­лит­ра; б) у пер­во­го гнома было 8/13 л, у осталь­ных  — по 6/13 л.