1. Тип Д8 C1 № 505658 

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Формулы двойного угла
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
а) Решите уравнение 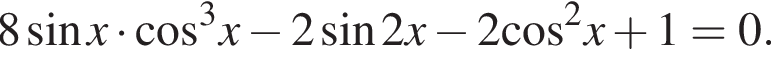
б) Найдите все корни на промежутке 
Решение. a) Решим уравнение:




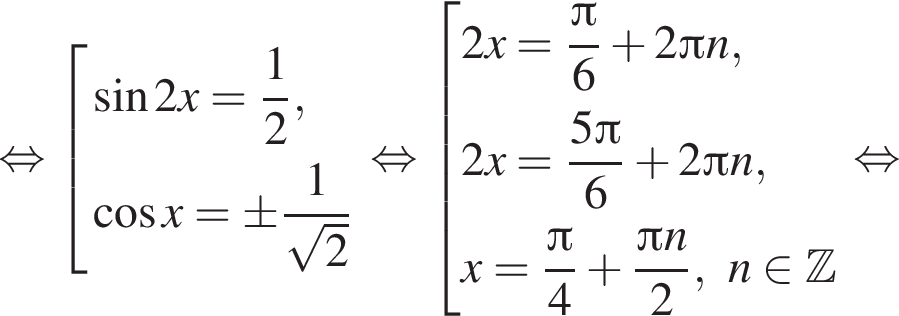


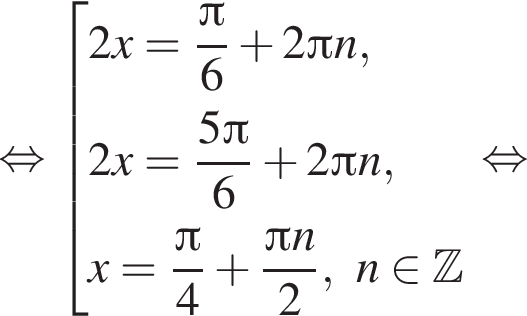

б) Выборка корней.



Покажем, что 
Действительно, 

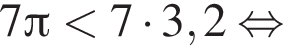

Ответ: а) 


б) ![]()
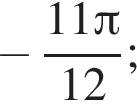
![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а) 





б) ![]()
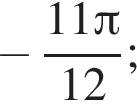
![]()
505658
а) 





б) ![]()
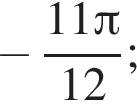
![]()
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Формулы двойного угла
 то диагонали ромба равны
то диагонали ромба равны  Чтобы найти вторую диагональ, решим уравнение
Чтобы найти вторую диагональ, решим уравнение  (это теорема Пифагора, дающая квадрат стороны ромба, примененная к треугольникам ABQ и CBQ, где Q — вершина ромба, лежащая на ребре BB1). Находим:
(это теорема Пифагора, дающая квадрат стороны ромба, примененная к треугольникам ABQ и CBQ, где Q — вершина ромба, лежащая на ребре BB1). Находим:  откуда вторая диагональ ромба равна
откуда вторая диагональ ромба равна 
 а до другой — не больше
а до другой — не больше  поэтому сечение не может быть ромбом. Аналогично разбирается случай ребер
поэтому сечение не может быть ромбом. Аналогично разбирается случай ребер 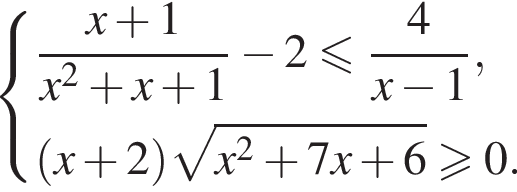




 являются числа: −1 и −3.
являются числа: −1 и −3.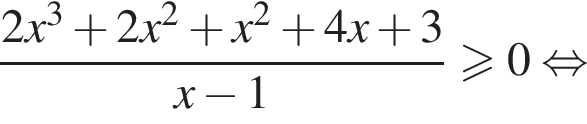



 при любом действительном значении x, так как
при любом действительном значении x, так как 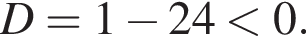 Итак, решениями первого неравенства является множество
Итак, решениями первого неравенства является множество  Теперь решим второе неравенство системы.
Теперь решим второе неравенство системы. 
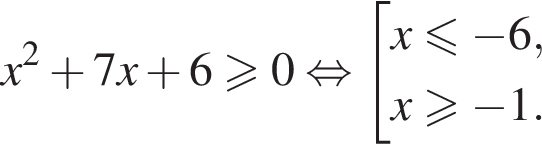

 Пересечением решений обоих неравенств будет множество
Пересечением решений обоих неравенств будет множество 
 Так как вписанный угол KAM и центральный угол KOM опираются на одну и ту же дугу KM в окружности
Так как вписанный угол KAM и центральный угол KOM опираются на одну и ту же дугу KM в окружности  В четырехугольнике ACLB углы ACL и ABL равны по
В четырехугольнике ACLB углы ACL и ABL равны по 



 Что и требовалось доказать.
Что и требовалось доказать.



 для этих значений одинаковы. Исследуем для начала, при каких значениях a функция
для этих значений одинаковы. Исследуем для начала, при каких значениях a функция  поэтому она имеет максимум при
поэтому она имеет максимум при  (значение 9) и минимум при
(значение 9) и минимум при  (значение
(значение  по три раза, а сами
по три раза, а сами  по два раза.
по два раза.  или
или 
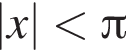 имеем
имеем  при прочих x имеем
при прочих x имеем 
 очевидно, принимает все положительные значения.
очевидно, принимает все положительные значения. то есть
то есть 

 число отлично от написанного над ним, то оно не меньше, чем
число отлично от написанного над ним, то оно не меньше, чем 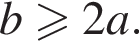 Кроме того, по крайней мере одно из чисел в этих группах отличается от
Кроме того, по крайней мере одно из чисел в этих группах отличается от  Итак,
Итак,  Наше утверждение доказано по индукции для всех
Наше утверждение доказано по индукции для всех  Если предположить, что 11-я строчка отлична от 12-й, то какое-то число в 12-й строчке будет больше, чем
Если предположить, что 11-я строчка отлична от 12-й, то какое-то число в 12-й строчке будет больше, чем  что невозможно.
что невозможно.