1. Тип Д8 C1 № 505634 
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Тригонометрические формулы суммы и разности аргументов, Формулы половинного аргумента
Уравнения, системы уравнений. Сложные тригонометрические уравнения, исследование ОДЗ
i
а) Решите уравнение: 
б)Найдите все корни на промежутке 
Решение. a) Ограничения на 
Для таких значений x будем иметь:
б) Выборку корней сделаем с помощью перебора различных значений 
При 
при 
при 
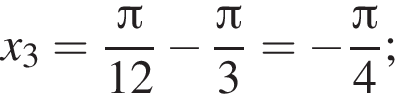При 
при 
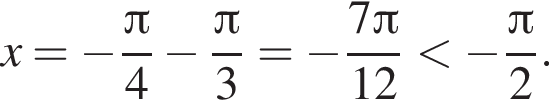
Дальнейшие поиски корней не имеют смысла.
Ответ: а) 
б) 
Замечание.
Нахождение корней заданного уравнения можно провести и так:
Полученные серии корней можно объединить в одну серию: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а) б)
б) 505634
а) б)
б) 
поэтому середина высоты DE (точка P) лежит на поверхности шара и противоположна E. Плоскость, перпендикулярная DE, параллельна плоскости основания пирамиды, поэтому является касательной плоскостью к шару. Следовательно, O совпадает с P.
поэтому 
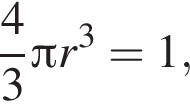то 
поэтому ответ 
Итак, решения первого неравенства есть множество 
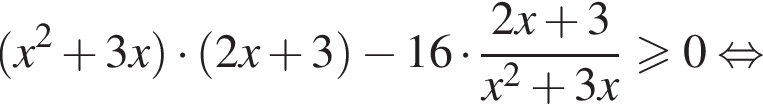
для всех 
поскольку 
будем иметь: 
значит, 
Так как треугольник AO2B равнобедренный (AO2 = O2B = R1), то
и 
равны, как вертикальные, и потому получаем: 
а значит точка O лежит на стороне AB. Лемма доказана.
и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:
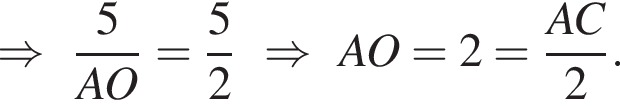
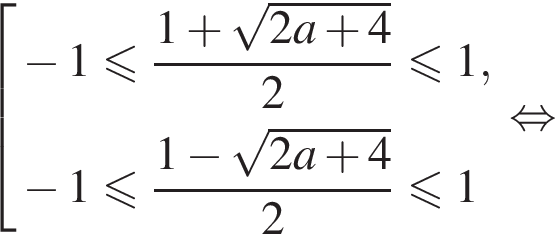
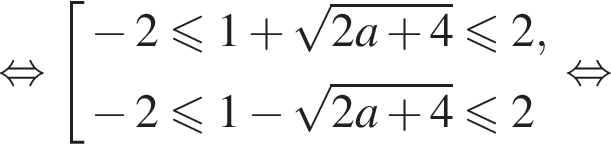
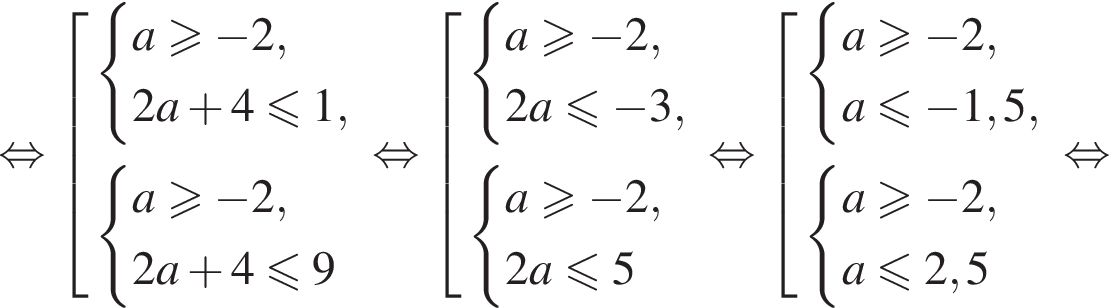
Тогда 
или 
(
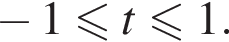
), или одновременное выполнение трех условий : 
Для нахождения интересующих нас значений a, удовлетворяющих этим трем условиям, решим систему неравенств:
(при всевозможных комбинациях знаков).
Обозначим один из корней за x, и будем рассматривать искомое выражение как многочлен 
степени 
произведение одночленов второй группы через 
каждый степени 
(в каждой группе встречаются всевозможные комбинации знаков всех слагаемых, кроме x) 
в силу определения этих многочленов.
поскольку при замене всех знаков при слагаемых в группе множителей, составляющих 
превратится в 
т. е. 
Докажем, что 
функцией от 
Разложим 
и 
в первый из которых входят делители P с коэффициентом 1 при y, а во второй — с коэффициентом –1. Очевидно, что 
Тогда 
— это тоже самое число. Итак, всё произведение есть полный квадрат.