1. Тип Д8 C1 № 521750 

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы половинного аргумента
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 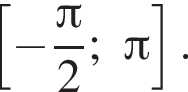
Решение. а) Обозначая  имеем
имеем 
![]() или
или ![]() (что невозможно). Значит,
(что невозможно). Значит,
 и
и 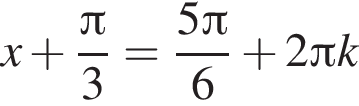
 и
и 
б) На указанном отрезке лежат 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
521750
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы половинного аргумента
 Тогда указанная плоскость — это плоскость
Тогда указанная плоскость — это плоскость  которая перпендикулярна главной диагонали куба.
которая перпендикулярна главной диагонали куба.  с перпендикулярными диагоналями (поскольку
с перпендикулярными диагоналями (поскольку  и
и  ). Тогда
). Тогда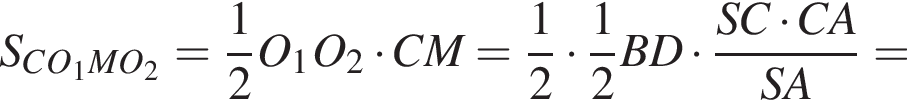




 Преобразуем его на ОДЗ и применим метод рационализации.
Преобразуем его на ОДЗ и применим метод рационализации.







 По теореме Фалеса
По теореме Фалеса  и Значит,
и Значит,  По свойству биссектрисы
По свойству биссектрисы  откуда
откуда  что и требовалось.
что и требовалось.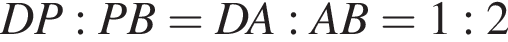 по свойству биссектрисы. Значит,
по свойству биссектрисы. Значит,
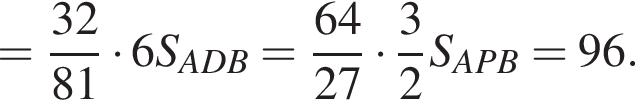




 Нужно найти наибольшее и наименьшее значение выражения
Нужно найти наибольшее и наименьшее значение выражения  То есть
То есть 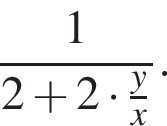 Значит, нужно установить границы выражения
Значит, нужно установить границы выражения 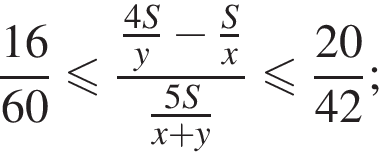



 откуда
откуда  откуда
откуда 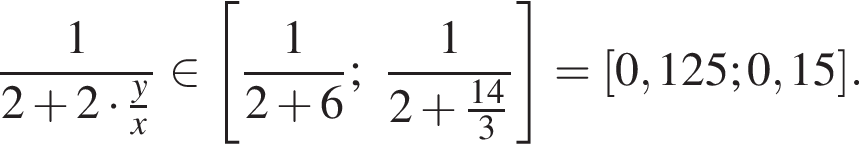 Итак, ответ от 12,5% до 15%.
Итак, ответ от 12,5% до 15%. Тогда нужно, чтобы
Тогда нужно, чтобы 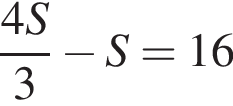 и
и  что выполняется одновременно при
что выполняется одновременно при 
 Тогда нужно, чтобы
Тогда нужно, чтобы  и
и  что выполняется одновременно при
что выполняется одновременно при 

 и
и  получим уравнение
получим уравнение 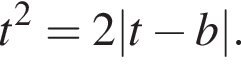
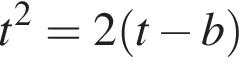 имело единственный корень. Приравнивая к нулю его дискриминант, получаем
имело единственный корень. Приравнивая к нулю его дискриминант, получаем  Аналогично при
Аналогично при  касание будет с другой стороны.
касание будет с другой стороны. 


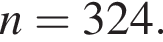
 фотографий.
фотографий.