1. Тип Д8 C1 № 521678 

Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Использование косвенных методов
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
Решение. а) Поскольку  при всех
при всех ![]() уравнение может выполняться только при одновременном выполнении следующих условий:
уравнение может выполняться только при одновременном выполнении следующих условий:  Уравнение
Уравнение  дает
дает  и такие значения подходят во все остальные уравнения.
и такие значения подходят во все остальные уравнения.
б) На указанном промежутке лежит 
Ответ: а)  б)
б) 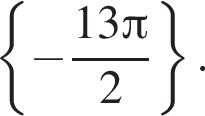
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 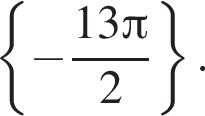
 б)
б) 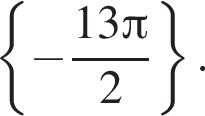
521678
а)  б)
б) 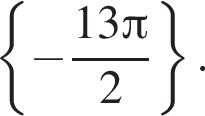
 б)
б) 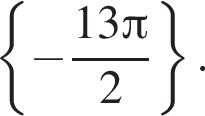
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Использование косвенных методов

 тогда
тогда 


 Поскольку
Поскольку  треугольник MPN — прямоугольный. Значит, и плоскости содержащих их граней перпендикулярныы,поскольку грани пересекаются по некоторой прямой, проходящей через P и параллельной AB и DE, поэтому MP и NP перпендикулярны прямой пересечения этих плоскостей.
треугольник MPN — прямоугольный. Значит, и плоскости содержащих их граней перпендикулярныы,поскольку грани пересекаются по некоторой прямой, проходящей через P и параллельной AB и DE, поэтому MP и NP перпендикулярны прямой пересечения этих плоскостей.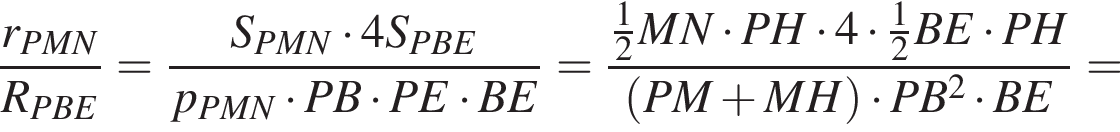
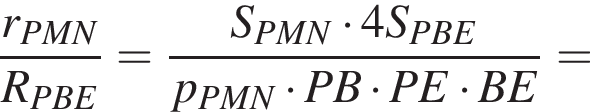
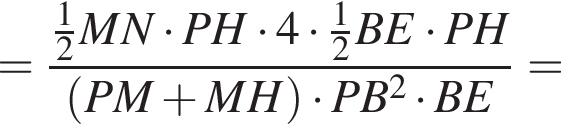







 и приведем все логарифмы к основанию 2,учитывая что
и приведем все логарифмы к основанию 2,учитывая что  имеем:
имеем:








 Опустим перпендикуляр KH на AC и отметим на AC точку
Опустим перпендикуляр KH на AC и отметим на AC точку  Тогда в треугольнике CKE высота совпадает с медианой и
Тогда в треугольнике CKE высота совпадает с медианой и  Значит, у треугольников
Значит, у треугольников 
 поэтому построенная таким образом точка совпадает с точкой E, перпендикуляр- с перпендикуляром из задачи и точка
поэтому построенная таким образом точка совпадает с точкой E, перпендикуляр- с перпендикуляром из задачи и точка 
 откуда
откуда  По формуле для биссектрисы имеем
По формуле для биссектрисы имеем 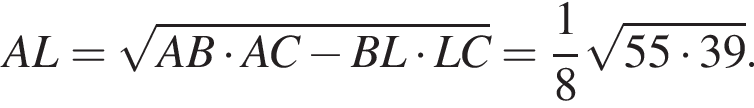 По теореме о пересекающихся хордах
По теореме о пересекающихся хордах 

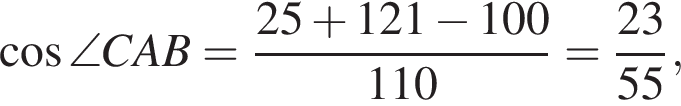 Значит,
Значит,  откуда
откуда 

 миллионов рублей. Выплаты за первые месяцы составили
миллионов рублей. Выплаты за первые месяцы составили 
 а дальше выплаты уменьшались на
а дальше выплаты уменьшались на 


 Тогда имеем
Тогда имеем  и
и  Складывая эти уравнения, находим
Складывая эти уравнения, находим  Подставляя это во второе уравнение, получаем после преобразований уравнение
Подставляя это во второе уравнение, получаем после преобразований уравнение  с корнями
с корнями  В первом случае
В первом случае 


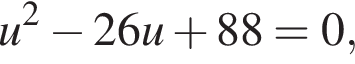
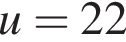 или
или  или
или  Второе невозможно, а первое дает лишь один ответ
Второе невозможно, а первое дает лишь один ответ  (угадано по теореме Виета).
(угадано по теореме Виета). имеем
имеем 
 или
или  Подставляя это во второе уравнение системы, находим соответственно
Подставляя это во второе уравнение системы, находим соответственно  или
или 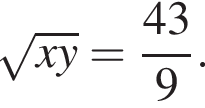 Первое дает лишь один ответ
Первое дает лишь один ответ  (угадано по теореме Виета).Второе дает два ответа, поскольку числа
(угадано по теореме Виета).Второе дает два ответа, поскольку числа  являются корнями квадратного уравнения
являются корнями квадратного уравнения  у которого действительно есть два положительных различных корня.
у которого действительно есть два положительных различных корня.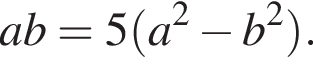 Поделив на
Поделив на  у которого нет рациональных корней, поэтому таких a и b не найдется.
у которого нет рациональных корней, поэтому таких a и b не найдется.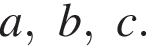 Получаем уравнение
Получаем уравнение  Ясно, что c кратно 5, получаем два случая.
Ясно, что c кратно 5, получаем два случая. что невозможно, поскольку
что невозможно, поскольку 
 то есть
то есть  Это можно записать в виде
Это можно записать в виде  причем
причем  то есть второй множитель — от
то есть второй множитель — от 
