1. Тип Д8 C1 № 506044 

Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения, Уравнения смешанного типа, Показательные уравнения
Методы алгебры: Формулы двойного угла
Уравнения, системы уравнений. Сложные уравнения смешанного типа
i
а) Решите уравнение 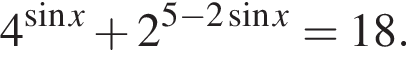
б) Найдите все корни на промежутке 
Решение. а)

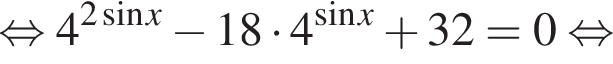


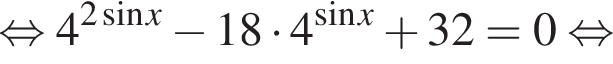
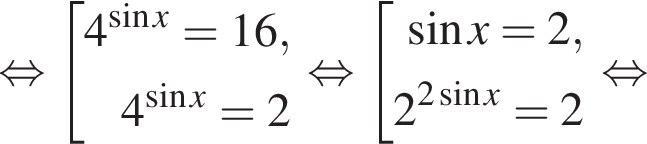


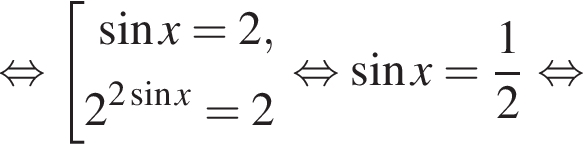

Уравнение  решений не имеет.
решений не имеет.
б)


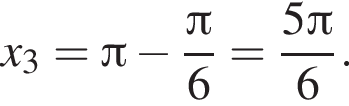
Ответ: а)  б)
б) ![]()
![]()
![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 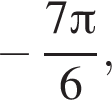


 б)
б) 506044
а)  б)
б) 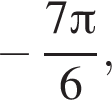


 б)
б) Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения, Уравнения смешанного типа, Показательные уравнения
Методы алгебры: Формулы двойного угла
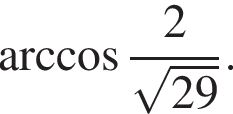
 Проведем высоту SC треугольника SAB. Тогда
Проведем высоту SC треугольника SAB. Тогда  и
и  поэтому
поэтому  и
и 
 откуда
откуда 
 и объем конуса равен
и объем конуса равен 









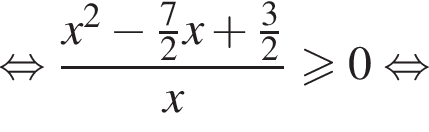









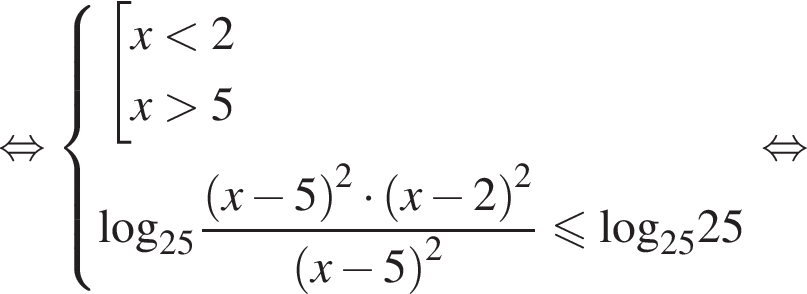


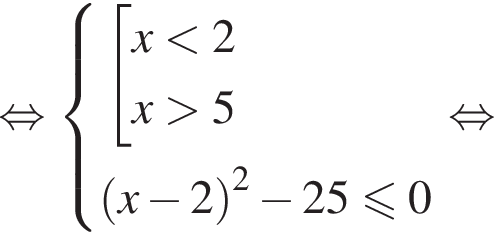



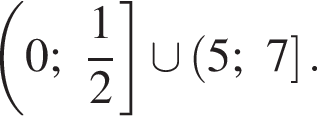
 — прямоугольная трапеция, в которой
— прямоугольная трапеция, в которой 

 и (опуская высоту из
и (опуская высоту из  откуда
откуда  — трапеция, в которой
— трапеция, в которой  откуда
откуда 




 всегда является корнем этого уравнения, а другие целые числа его корнями не являются. Поэтому можно поделить уравнение на
всегда является корнем этого уравнения, а другие целые числа его корнями не являются. Поэтому можно поделить уравнение на  У полученного уравнения должно не быть корней. Обозначим
У полученного уравнения должно не быть корней. Обозначим  Заметим, что на промежутке
Заметим, что на промежутке 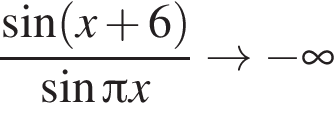 при
при 
 при
при 
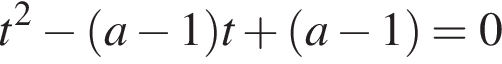 не должно иметь корней. То есть
не должно иметь корней. То есть 


