2. Тип Д10 C2 № 505931 
Сложная стереометрия. Многогранники
i
Решение. 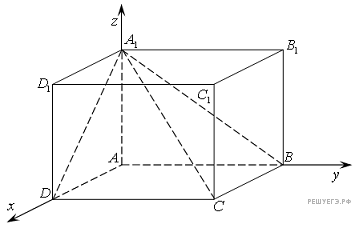 1) Координатно-векторный подход к решению задачи.
1) Координатно-векторный подход к решению задачи.
Нам требуется найти величину конкретного двугранного угла, а именно того двугранного угла, который образуется при пересечении двух плоскостей:  и
и  При пересечении двух плоскостей образуется четыре двугранного угла, по сути две пары равных между собой двугранных углов.
При пересечении двух плоскостей образуется четыре двугранного угла, по сути две пары равных между собой двугранных углов.
Угол между двумя плоскостями, а в нашем случае это — угол между плоскостями  и
и  будет вычислен как угол между нормальными векторами этих плоскостей
будет вычислен как угол между нормальными векторами этих плоскостей  и
и  Обозначим его
Обозначим его  А угол между двумя векторами заведомо не больше чем
А угол между двумя векторами заведомо не больше чем 
Поскольку при пересечении двух плоскостей, образуется, как сказано выше, две пары равных между собой двугранных углов, нам нужно будет выбрать, который угол будет искомым: угол  или
или 
Именно поэтому при вычислении угла между двумя плоскостями используют формулу:

Где  и
и  — соответствующие координаты нормальных векторов плоскостей.
— соответствующие координаты нормальных векторов плоскостей.
Косинус угла между нормальными векторами плоскостей  и
и  в нашем случае получится положительным. Однако с учетом конкретной ситуации мы будем должны взять этот косинус с отрицательным знаком, поскольку искомый угол тупой.
в нашем случае получится положительным. Однако с учетом конкретной ситуации мы будем должны взять этот косинус с отрицательным знаком, поскольку искомый угол тупой.
Введем декартову систему координат как показано на рис. Ребро куба примем за 1.
Будем искать уравнения плоскостей  и
и 
Координаты нужных точек будут следующими:

Найдем уравнение плоскости 



Итак, искомое уравнение имеет вид:  или
или  Координаты нормального вектора этой плоскости:
Координаты нормального вектора этой плоскости: 
Найдем уравнение плоскости 



Искомое уравнение имеет вид:  или
или  Координаты нормального вектора этой плоскости:
Координаты нормального вектора этой плоскости: 

Так как искомый угол заведомо тупой, то 
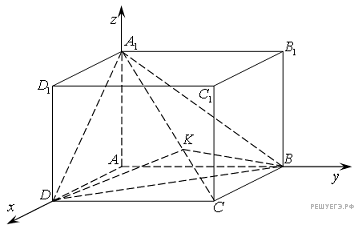 2) Элементарно-геометрический подход к решению. Проведем отрезки
2) Элементарно-геометрический подход к решению. Проведем отрезки  Пусть
Пусть  — линейный угол упомянутого двугранного угла,
— линейный угол упомянутого двугранного угла,  И пусть ребро куба равно 1. Тогда
И пусть ребро куба равно 1. Тогда 
Заметим, что  поскольку
поскольку 
Рассмотрим 

 подобны, так как они прямоугольные,
подобны, так как они прямоугольные,  как углы, заключенные между взаимно перпендикулярными прямыми. Следовательно,
как углы, заключенные между взаимно перпендикулярными прямыми. Следовательно,  Аналогично
Аналогично 
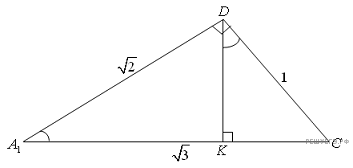
В  по теореме косинусов имеем:
по теореме косинусов имеем: 




Ответ: 
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: 

и выделим левой части уравнения полный квадрат суммы
Имеем:
или
то имеем:
то
откуда имеем:
являются решениями системы, а вместе с ней и исходного уравнения.
при помощи единичной окружности (см. рис.).
б)
 PDF-версии:
PDF-версии: