4. Тип Д15 C4 № 505885 
Сложная планиметрия. Комбинации фигур
i
Дан прямоугольный треугольник MNK с катетами 5 и 12. Треугольник KNJ — равносторонний, причем точка J и точка M ледат по разные стороны от прямой NK. Найдите расстояние от центра вписанной окружности в MNK до центра вписанной в KNJ окружности.
Решение. Докажем сначала лемму:
Пусть две точки лежат по разные стороны от прямой, расстояния от них до прямой равны  и
и  а расстояние между их проекциями на эту прямую равно d. Тогда расстояние между точками равно
а расстояние между их проекциями на эту прямую равно d. Тогда расстояние между точками равно 
Доказательство. Опустим из одной точки перпендикуляр на прямую и продлим его до пересечения с прямой, параллельной данной и проходящей через вторую точку. Тогда точка пересечения вместе с начальными двумя точками образуют прямоугольный треугольник, и утверждение леммы следует из теоремы Пифагора.
Вычислим радиусы вписанных окружностей треугольника MNK и равностороннего треугольника с данной стороной, а также отрезки, на которые стороны этих треугольников делятся точками касания с вписанной окружностью.

Если опустить из центра перпендикуляры на катеты, образуется квадрат со стороной 2, поэтому некоторые отрезки равны двум. Остальные равны  и
и 
Для равностороннего треугольника со стороной a радиус равен  а все отрезки на сторонах равны
а все отрезки на сторонах равны 
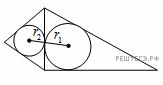
Перейдем к решению задачи. Возможны три случая — треугольник построен на меньшем катете, на большем катете, на гипотенузе. В каждом случае будем применять лемму и ужесделанные вспомогательные вычисления.
Если на меньшем катете, то 
 а перпендикуляры на меньший катет падают на расстояниях 2 и
а перпендикуляры на меньший катет падают на расстояниях 2 и  от вершины прямого угла, и расстояние между ними будет
от вершины прямого угла, и расстояние между ними будет 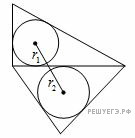
 По лемме расстояние получится
По лемме расстояние получится 
Если на большем катете, то 
 а перпендикуляры на меньший катет падают на расстояниях 2 и 6 от вершины прямого угла, и расстояние между ними будет 4.
а перпендикуляры на меньший катет падают на расстояниях 2 и 6 от вершины прямого угла, и расстояние между ними будет 4.
По лемме расстояние получится 
Если на гипотенузе, то 
 а перпендикуляры на меньший катет падают на расстояниях 3 и
а перпендикуляры на меньший катет падают на расстояниях 3 и  от вершины большего острого угла, и расстояние между ними будет
от вершины большего острого угла, и расстояние между ними будет 
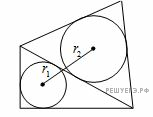 По лемме расстояние получится
По лемме расстояние получится 
Ответ: 


Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |

Ясно, что областью определения функции
будут значения x, при которых определён
Он определен при всех значениях
т. е. при
Таким образом, ограничения на искомые значения
Действительно, при
имеем:
выражением
А условие
указывает на способ получения значений функций f, зная значения
Говоря по-другому, нам предстоит решить уравнение
относительно
Решим его:
б)
 PDF-версии:
PDF-версии: