1. Тип 13 № 548563 

Классификатор алгебры: Сравнение чисел, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Уравнения. Тригонометрические уравнения, сводимые к квадратным
i
а) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение.







б) Отберем корни при помощи единичной тригонометрической окружности (см. рис.). На заданном отрезке лежат корни 
Ответ: а) б)
б)
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а) б)
б)
 б)
б)
548563
а) б)
б)
 б)
б)
Классификатор алгебры: Сравнение чисел, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения











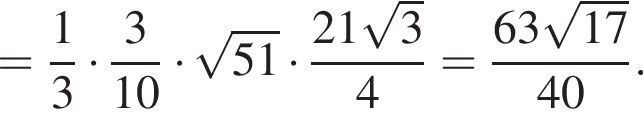












 Так как C1A1 — медиана в прямоугольном треугольнике BC1C, то
Так как C1A1 — медиана в прямоугольном треугольнике BC1C, то 


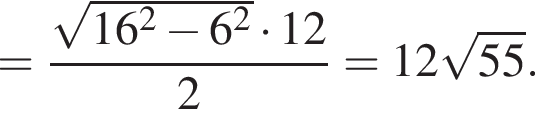






 первое уравнение системы принимает вид:
первое уравнение системы принимает вид:  или
или  откуда
откуда 
 принимает вид
принимает вид  откуда x = 0 или
откуда x = 0 или 
 принимает вид
принимает вид  откуда
откуда  или
или 
 При положительных a корень
При положительных a корень  условие
условие 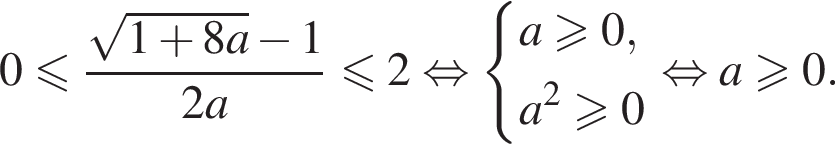


 не равны нулю при положительных a и совпадают при
не равны нулю при положительных a и совпадают при


 Если после перекладывания оно стало равно 16 г, то масса кучки
Если после перекладывания оно стало равно 16 г, то масса кучки  Значит, добавленная гирька была массой
Значит, добавленная гирька была массой  что невозможно, поскольку такая гирька только одна.
что невозможно, поскольку такая гирька только одна. — нецелое число граммов.
— нецелое число граммов. Значит, была добавлена гирька весом
Значит, была добавлена гирька весом  Нужно сделать n как можно большим. Заметим, что даже если выбрать гирьки самой маленькой массы, n гирек будут весить
Нужно сделать n как можно большим. Заметим, что даже если выбрать гирьки самой маленькой массы, n гирек будут весить  поэтому
поэтому  Значит, масса добавленной гирьки не меньше чем
Значит, масса добавленной гирьки не меньше чем  Отсюда
Отсюда  то есть
то есть 
 тогда все условия будут выполнены: средняя масса 23 грамма выросла до 24 граммов.
тогда все условия будут выполнены: средняя масса 23 грамма выросла до 24 граммов.