1. Тип Д8 C1 № 508683 

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. а) Последовательно получаем:





б) Отбор корней сделаем с помощью единичной окружности.




Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
508683
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла

 — искомое сечение. Докажем это.
— искомое сечение. Докажем это. по условию,
по условию,  по построению, следовательно,
по построению, следовательно,  — по свойству транзитивности отношения параллельности.
— по свойству транзитивности отношения параллельности. значит, A = BF. Прямоугольные треугольники A1AE и B1BF равны по двум катетам, следовательно, A1 = B1F.
значит, A = BF. Прямоугольные треугольники A1AE и B1BF равны по двум катетам, следовательно, A1 = B1F.








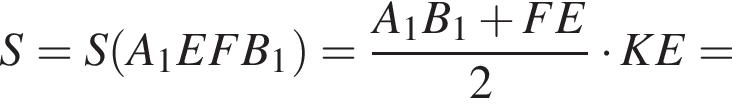

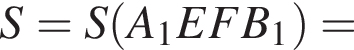
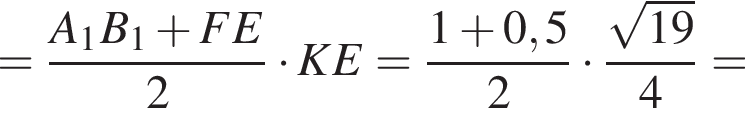






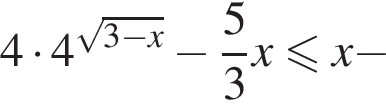






 не меньше 1, а правая же часть — не больше 1. Следовательно, неравенство выполнимо при равенстве обеих частей, т. е. лишь при
не меньше 1, а правая же часть — не больше 1. Следовательно, неравенство выполнимо при равенстве обеих частей, т. е. лишь при  Так как BK || AC, то
Так как BK || AC, то  т. е.
т. е.  Следовательно, около
Следовательно, около 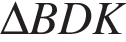 можно описать окружность с центром в точке Н и радиусом R = BH = KH = DH. Итак,
можно описать окружность с центром в точке Н и радиусом R = BH = KH = DH. Итак, 
 т. е.
т. е. 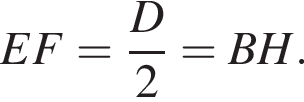 Отсюда вывод: в равнобочной трапеции, у которого диагонали взаимно перпендикулярны, высота равна средней линии этой же трапеции.
Отсюда вывод: в равнобочной трапеции, у которого диагонали взаимно перпендикулярны, высота равна средней линии этой же трапеции.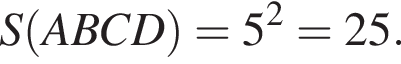
 Значит,
Значит, 
 как внутренние накрест лежащие при параллельных ВА, СD и секущей ВD. Следовательно,
как внутренние накрест лежащие при параллельных ВА, СD и секущей ВD. Следовательно,  В таком случае в
В таком случае в  где
где 
 — равнобедренный, т. е. BH = DH, что и требовалось доказать.
— равнобедренный, т. е. BH = DH, что и требовалось доказать. Определите срок хранения вклада.
Определите срок хранения вклада. раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.
раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится. месяцев увеличится в
месяцев увеличится в  раза.
раза. 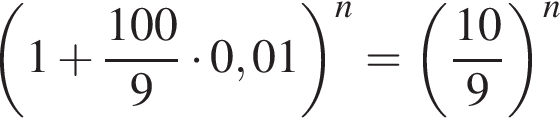 и
и 









 и
и  При этих значениях k и m система примет вид:
При этих значениях k и m система примет вид: 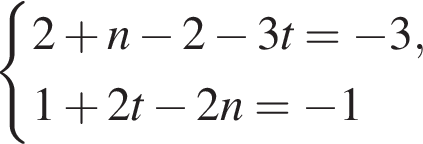
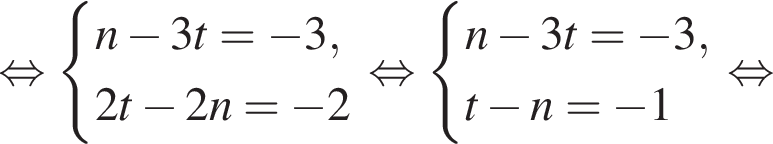

 вклад в банке на хранении был 7 месяцев. При найденных значениях
вклад в банке на хранении был 7 месяцев. При найденных значениях  действительно равно нулю.
действительно равно нулю. справедливо для всех действительных x.
справедливо для всех действительных x. при всех
при всех  то есть
то есть 
 при всех
при всех  то есть
то есть 
 процентов голосов, при этом
процентов голосов, при этом  Понятно, что партии 1 и 2 не пройдут в Думу, иначе для каждой из них не найдется двух других партий с меньшим числом голосов. Значит,
Понятно, что партии 1 и 2 не пройдут в Думу, иначе для каждой из них не найдется двух других партий с меньшим числом голосов. Значит,  Следовательно,
Следовательно,  (по условию), при том, что число голосов упорядочено по возрастанию. Если третья партия не прошла в Думу, то
(по условию), при том, что число голосов упорядочено по возрастанию. Если третья партия не прошла в Думу, то  если прошла, то
если прошла, то 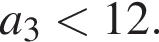


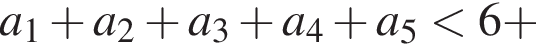

 если
если  то
то  что невозможно,
что невозможно, →
→ 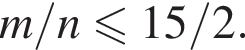 Приведем пример, когда значение 7,5 достигается:
Приведем пример, когда значение 7,5 достигается: 