1. Тип Д8 C1 № 505700 

Классификатор алгебры: Тригонометрические уравнения, Уравнения смешанного типа
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.3 Иррациональные уравнения
Уравнения, системы уравнений. Сложные тригонометрические уравнения, исследование ОДЗ
i
а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. a) Найдем ограничения на ![]()



Отсюда получим и часть решения уравнения. Таковыми будут числа вида: 
Остальная же часть решения содержится среди решений уравнения  Ясно, что ими будут числа
Ясно, что ими будут числа 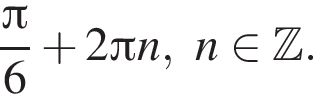
б) Выборка корней. Заданному отрезку принадлежат только два корня: ![]() и
и ![]()
Ответ: а)  б)
б) ![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 505700
а)  б)
б) 
 б)
б) Классификатор алгебры: Тригонометрические уравнения, Уравнения смешанного типа
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.3 Иррациональные уравнения



 Из третьего уравнения:
Из третьего уравнения:  Подставляя найденные значения a и b в первое уравнение, найдем c.
Подставляя найденные значения a и b в первое уравнение, найдем c.  Далее:
Далее:




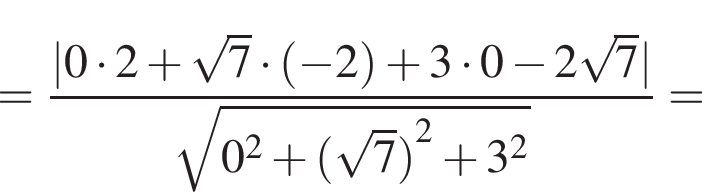













 Это — с одной стороны. А с другой же стороны,
Это — с одной стороны. А с другой же стороны,  где
где 




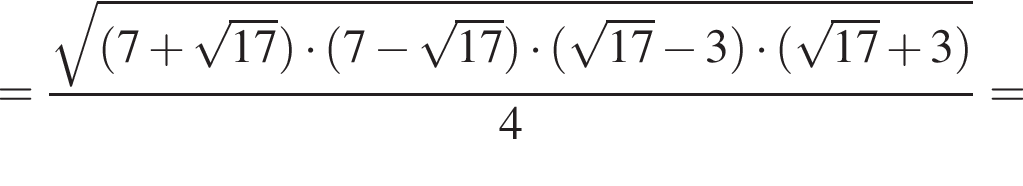



 К этой формуле можно прийти методом удвоения медианы. Если она забыта, ее можно восстановить легко и просто. И вот каким образом.
К этой формуле можно прийти методом удвоения медианы. Если она забыта, ее можно восстановить легко и просто. И вот каким образом. а его сторонами будут стороны треугольника длиной a и b. Как известно, сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Поскольку противолежащие стороны параллелограмма равны, то будет выполнено равенство:
а его сторонами будут стороны треугольника длиной a и b. Как известно, сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Поскольку противолежащие стороны параллелограмма равны, то будет выполнено равенство:  Отсюда:
Отсюда: 

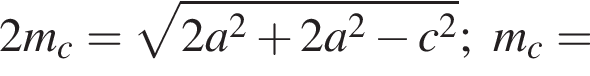


 Для таких
Для таких 
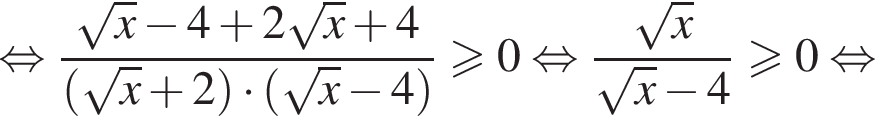

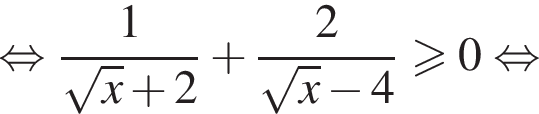
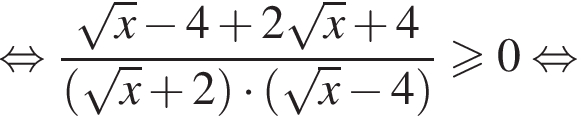



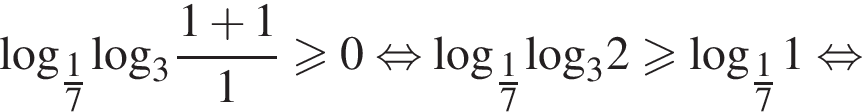







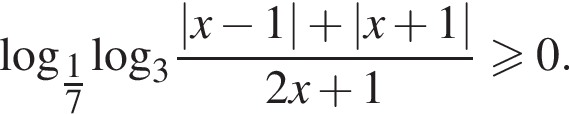





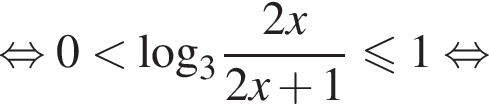




 при
при  невыполнимо. Следовательно, решения исходной системы
невыполнимо. Следовательно, решения исходной системы 

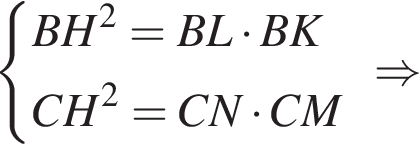

 откуда
откуда  Выразим различными способами площадь треугольника ABC.
Выразим различными способами площадь треугольника ABC.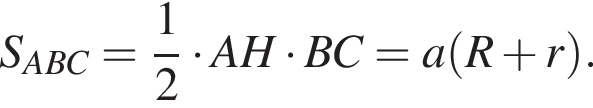


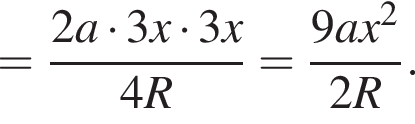









 ), получим:
), получим: 



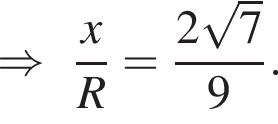

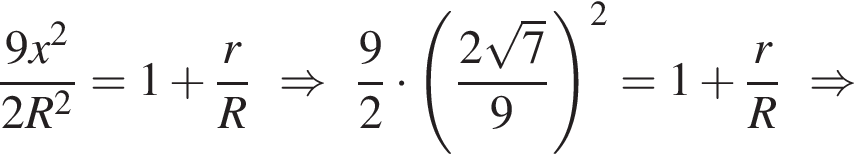




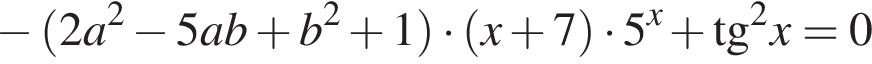












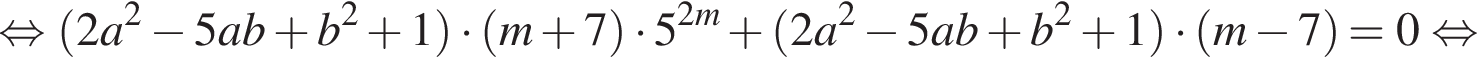


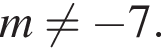 Действительно, если
Действительно, если  то
то  тогда как
тогда как  Следовательно, мы вправе разделить обе части равенства
Следовательно, мы вправе разделить обе части равенства  на
на 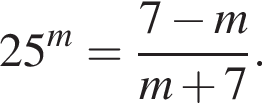 Это равенство имеет место при
Это равенство имеет место при 
 есть монотонно возрастающая функция, g(m) — монотонно убывающая. Cледовательно, равенство f (m)=
есть монотонно возрастающая функция, g(m) — монотонно убывающая. Cледовательно, равенство f (m)= 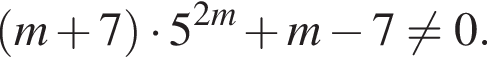
 Коли это так, то равенство (***) примет вид:
Коли это так, то равенство (***) примет вид:  что возможно лишь при одновременном выполнении двух условий:
что возможно лишь при одновременном выполнении двух условий:  и
и 
 при которых условие
при которых условие  выполняется как при
выполняется как при  так и при
так и при 












 то
то 




 Полученным значениям а будут соответствовать значения
Полученным значениям а будут соответствовать значения  в соответствии с равенством
в соответствии с равенством 
 к равенству
к равенству  (не обязательно равносильный). При подстановке пары (2; 1) в систему
(не обязательно равносильный). При подстановке пары (2; 1) в систему  получим верные равенства:
получим верные равенства:  Такие же получим результаты, если проверим пару (-2; -1).
Такие же получим результаты, если проверим пару (-2; -1). при некотором натуральном
при некотором натуральном  но
но  (при этом
(при этом  из условия). Но наибольшими числами, меньшими D и делящимися на 1005 и 1006, являются числа
из условия). Но наибольшими числами, меньшими D и делящимися на 1005 и 1006, являются числа 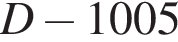 и
и 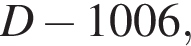 соответственно; поэтому
соответственно; поэтому 
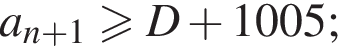 отсюда
отсюда 

 подходит, например, последовательность всех чисел, кратных 1005, но не кратных 97 (заметим, что 1005 не кратно 97).
подходит, например, последовательность всех чисел, кратных 1005, но не кратных 97 (заметим, что 1005 не кратно 97).