Найдите все значения a, при каждом из которых уравнение
имеет ровно один корень на отрезке [0; 1].
Решение. Исходное уравнение равносильно уравнению
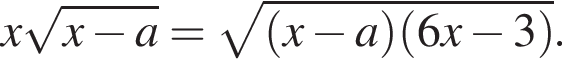
Рассмотрим два случая.
Первый случай: 
Получаем 
при 
Второй случай: 
при условии 
Получаем:
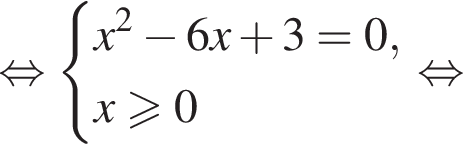
Для корня 
условие принимает вид 
откуда 
То есть в этом случае при
Корень уравнения принадлежит отрезку [0; 1] при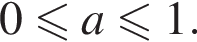 
Корни уравнения и совпадают при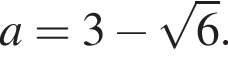 
Таким образом, исходное уравнение имеет ровно один корень на отрезке [0; 1] при 
и 
Ответ: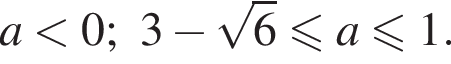 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| С помощью верного рассуждения получено множество значений а, отличающееся от искомого только включением/исключением точек a = 0 и/или a = 1 | 3 |
| В решении верно найдены корни
возможно, с исключением граничных точек ИЛИ верно пройдены все этапы решения, но неверно найдены граничные точки множества значений a из-за вычислительной ошибки | 2 |
| В решении верно найден один из корней
возможно, с исключением граничных точек | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
при 
и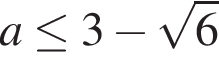 
,
или с учетом принадлежности корней указанному отрезку: 
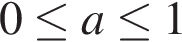и 