
В треугольнике ABC точки M и N лежат на сторонах AB и BC соответственно так, что  Окружность, вписанная в треугольник ABC, касается отрезка MN в точке K.
Окружность, вписанная в треугольник ABC, касается отрезка MN в точке K.
a) Докажите, что 
б) Найдите радиус окружности, вписанной в треугольник ABC, если 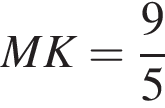 и
и 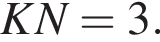
Решение. а) Пусть AM = 2x, MB = 3x, BN = 3y, NC = 2y. Тогда треугольники ABC и MBN подобны, и прямые MN и AC параллельны. Поскольку
 MN = 3t, AC = 5t. По свойству описанного четырёхугольника,
MN = 3t, AC = 5t. По свойству описанного четырёхугольника,

тогда

Отсюда 
 Что и требовалось доказать.
Что и требовалось доказать.
б) Пусть P — точка касания окружности со стороной AC, O — центр окружности. Тогда прямые OK и MN перпендикулярны, прямые OP и AC перпендикулярны, прямые MN и AC параллельны. Тогда точки K, O и P лежат на одной прямой, и AMKP — прямоугольная трапеция. Пусть AP = x. Заметим, что

откуда PC = 8 − x. Тогда 
 По теореме Пифагора
По теореме Пифагора

Из другой прямоугольной трапеции получаем, что


Отсюда  тогда радиус окружности, вписанной в треугольник ABC, равен 3.
тогда радиус окружности, вписанной в треугольник ABC, равен 3.
Ответ: б) 3.
Приведем решение пункта б) Ивана Иванова.
Треугольники ABC и MBN подобны с коэффициентом подобия ![]() тогда
тогда  тогда:
тогда:

Пусть F — точка касания окружности и стороны AB, E — точка касания окружности и стороны CB, тогда 
 Отрезки BF и BE равны как отрезки касательных, проведенных из одной точки, следовательно,
Отрезки BF и BE равны как отрезки касательных, проведенных из одной точки, следовательно,

По доказанному в пункте а)  Решая систему уравнений, получим AB = 17, BC = 15.
Решая систему уравнений, получим AB = 17, BC = 15.
Для треугольника ABC выполняется равенство  следовательно, он прямоугольный, и его площадь равна
следовательно, он прямоугольный, и его площадь равна  С другой стороны,
С другой стороны, 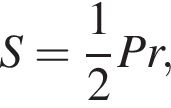 тогда
тогда

| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |