Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Решение. Запишем уравнение в виде 
и построим графики левой и правой частей. Из графиков, учитывая, что несовпадающие прямые имеют не более одной общей точки, получим следующее.
При a = 0 нет решений, т. к. левая часть равна 0, а правая не больше −2.
При 
два решения есть тогда и только тогда, когда точка A лежит ниже точки B:
то есть при 
При 
два решения есть тогда и только тогда, когда точка C лежит ниже точки D: 
то есть при 
Приведем аналитическое решение.
Раскроем модуль при 
получим
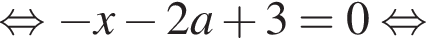
Найденное решение должно лежать в рассматриваемом промежутке: 
то есть
При 
имеем:
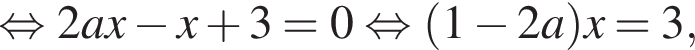
полученное уравнение не имеет решений при 
при 
имеет единственное решение 
Найденное решение должно лежать в рассматриваемом промежутке:
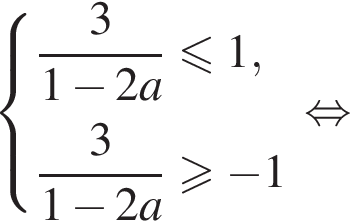
При 
имеем:
Найденное решение должно лежать в рассматриваемом промежутке, поэтому 
то есть
Таким образом, уравнение имеет ровно два различных решения 
или 
Ответ: или
Приведём решение Елизаветы Зелененькой (Москва).
Решим задачу графическим методом в координатах (x; a). Прямые x + 1 = 0 и x − 1 = 0 разбивают координатную плоскость три области, в каждой из которых модули раскрываются согласно приведенной ниже таблице.
| Выражение | 1 область | 2 область | 3 область |
| x + 1 | − | + | + |
| x − 1 | − | − | + |
Найдем вид уравнения в каждой из областей. В первой первой области:
это уравнение прямой с коэффициентом наклона k = −0,5. Во второй области:
Полученное уравнение задает гиперболу, вертикальной асимптотой которой является ось ординат. В третьей области:
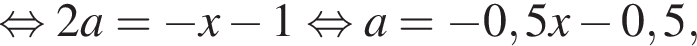
это уравнение прямой с коэффициентом наклона k = −0,5. Построим график уравнения (см. рис.), отметим, что гипербола пересекает прямые в точках (−1; 2) и (1; −1).
Исходное уравнение имеет два решения тогда и только тогда, когда горизонтальная прямая 
пересекает график в двух точках, то есть лежит выше точки пересечения гиперболы с первой прямой либо ниже точки пересечения гиперболы со второй прямой. Таким образом, или при