Ре­ше­ние. a)  

Серия кор­ней со­дер­жит­ся в серии кор­ней

б)  Ясно, что в за­дан­ный про­ме­жу­ток по­па­да­ют корни: Кроме того, будет еще один ко­рень

Ответ: а) б)

Ре­ше­ние. По­стро­е­ние се­че­ния.

Стро­им по­сле­до­ва­тель­но:

1.  От­ре­зок KL,

2.  От­ре­зок

3.  От­ре­зок

4.  От­ре­зок MN.

До­ка­жем, что LMNK  — ис­ко­мое се­че­ние.

Во-пер­вых, LM || SA, KN || SA, сле­до­ва­тель­но, LM || KN. По­сколь­ку через две па­рал­лель­ные пря­мые про­хо­дит одна и толь­ко одна плос­кость, то точки L, M, N, K при­над­ле­жат одной плос­ко­сти.

Во-вто­рых, SA || LM по по­стро­е­нию, зна­чит, SA || (LM); ана­ло­гич­но KL || BC (по по­стро­е­нию), сле­до­ва­тель­но, BC || (LM).

Те­перь до­ка­жем, что LMNK  — пря­мо­уголь­ник.

Про­ве­дем бис­сек­три­су угла BAC. Оче­вид­но, она прой­дет через точку H, раз­де­лит от­ре­зок BC на два рав­ных от­рез­ка (обо­зна­чим точку пе­ре­се­че­ния P), будет пер­пен­ди­ку­ляр­ной к от­рез­ку BC.

Со­еди­ним точки S и P от­рез­ком.

Далее мы впра­ве утвер­ждать, что при зер­каль­ной сим­мет­рии от­но­си­тель­но плос­ко­сти SA за­дан­ная пи­ра­ми­да пе­рей­дет сама на себя. При­чем, вер­ши­ны пи­ра­ми­ды A и S, точка P пе­рей­дут сами в себя, вер­ши­на В пе­рей­дет в вер­ши­ну С и, на­о­бо­рот, точка С пе­рей­дет в точку В. Так как KL || BC, то точки К и L пе­рей­дут друг в друга (по тео­ре­ме Фа­ле­са будет спра­вед­ли­вым ра­вен­ство АК : КС = АL : LB), кроме того, АС  =  АВ по усло­вию. Ана­ло­гич­но и точки M и N пе­рей­дут друг в друга, по­сколь­ку при той же сим­мет­рии и пе­рей­дут друг на друга.

Тогда спра­вед­ли­вы ра­вен­ства: KN=LM, KM=LN.

Из ра­вен­ства от­рез­ков KN и LM, а также их па­рал­лель­но­сти (по­ка­за­но выше) сле­ду­ет, что че­ты­рех­уголь­ник LMNK  — па­рал­ле­ло­грамм, А так как у него равны диа­го­на­ли, то этот па­рал­ле­ло­грамм - пря­мо­уголь­ник.

Оста­лось вы­чис­лить пло­щадь пря­мо­уголь­ни­ка LMNK.

Так как   — рав­но­сто­рон­ний, то

В где

Так как KL || BC, то От­сю­да:

Из па­рал­лель­но­сти AS и ML сле­ду­ет, что

Ответ:

Ре­ше­ние. Рас­смот­рим вто­рое не­ра­вен­ство си­сте­мы. За­ме­тим, что чис­ли­тель дроби (левая часть не­ра­вен­ства), по­ло­жи­те­лен при всех зна­че­ния так как дис­кри­ми­нант под­ко­рен­но­го вы­ра­же­ния от­ри­ца­те­лен: А для того чтобы левая часть не­ра­вен­ства была не мень­ше 1, не­об­хо­ди­мо и до­ста­точ­но вы­пол­не­ние двух усло­вий: и Решим си­сте­му:

Од­на­ко, при зна­ме­на­тель левой части пер­во­го не­ра­вен­ства об­ра­ща­ет­ся в нуль. По­это­му даль­ней­шие наши ис­сле­до­ва­ния будем вести на мно­же­стве

Решим пер­вое не­ра­вен­ство на ука­зан­ном мно­же­стве. По­сколь­ку на то

По­сколь­ку на то на этом мно­же­стве А также на Зна­чит, на этом мно­же­стве

Таким об­ра­зом, ре­ше­ния ис­ход­ной си­сте­мы есть мно­же­ство (2; 3).

Ответ: (2; 3).

Ре­ше­ние. а)  Пусть тогда (рис. 1).

По тео­ре­ме си­ну­сов будем иметь:

В

В Так как

то

Зна­чит,

Ясно, что

б)  Пусть   — центр окруж­но­сти, опи­сан­ной около   — центр окруж­но­сти, опи­сан­ной около (Рис. 2).

Оче­вид­но, что точки и лежат на се­ре­дин­ном пер­пен­ди­ку­ля­ре к от­рез­ку BM. Пусть он пе­ре­се­ка­ет BM в точке D. Тогда

Наша за­да­ча  — найти длину от­рез­ка

Най­дем и ко­то­рые яв­ля­ют­ся ра­ди­у­са­ми на­зван­ных окруж­но­стей.

Нам по­на­до­бят­ся зна­че­ния си­ну­са и ко­си­ну­са угла BAM.

По след­ствию из тео­ре­мы си­ну­сов будем иметь:

В где по тео­ре­ме Пи­фа­горa по­лу­чим:

В ана­ло­гич­но

Ответ: а) б) 17.

Ре­ше­ние. При урав­не­ние при­мет вид:

По­ка­жем, что пра­вая часть по­след­не­го урав­не­ния от­ри­ца­тель­на. Дей­стви­тель­но, (не­ра­вен­ство оче­вид­ное). Сле­до­ва­тель­но, среди ис­ко­мых зна­че­ний а числа 0 нет.

При­ве­дем за­дан­ное урав­не­ние к виду

Рас­смот­рим функ­ции:

Функ­ция квад­ра­тич­ная, по­сколь­ку Вы­чис­лим чет­верть дис­кри­ми­нан­та квад­рат­но­го трех­чле­на:

Итак, стар­ший ко­эф­фи­ци­ент квад­рат­но­го трех­чле­на по­ло­жи­те­лен, чет­верть дис­кри­ми­нан­та равна нулю, зна­чит, функ­ция об­ра­ща­ет­ся в нуль при един­ствен­ном зна­че­нии х, а при осталь­ных же зна­че­ни­ях х

Те­перь рас­смот­рим функ­цию Ясно, что эта функ­ция об­ра­ща­ет­ся в нуль при при дру­гих же зна­че­ни­ях x, т. е. при

Для того чтобы за­дан­ное урав­не­ние имело хотя бы одно ре­ше­ние, не­об­хо­ди­мо и до­ста­точ­но, чтобы ра­вен­ство вы­пол­ня­лось хотя бы при одном зна­че­нии x. Таким зна­че­ни­ем будет число 2. И оно един­ствен­ное. Ис­ко­мое зна­че­ние а будет об­на­ру­же­но, если ре­шить урав­не­ние от­но­си­тель­но а:

До­пол­ни­тель­ное по­яс­не­ние. Гео­мет­ри­че­ская ин­тер­пре­та­ция си­ту­а­ции как-то вы­гля­дит так:

Ответ:

Ре­ше­ние. а)  Рас­по­ло­жим дву­знач­ные числа в клет­ках пря­мо­уголь­ни­ка вы­со­ты 9 и ши­ри­ны 10 (по го­ри­зон­та­ли от­кла­ды­ва­ем еди­ни­цы, по вер­ти­ка­ли  — де­сят­ки). Каж­дой по­пыт­ке Гриши со­от­вет­ству­ет кре­стик из пяти кле­ток: в цен­тре на­зван­ное им число, а по бокам че­ты­ре числа, от­ли­ча­ю­щи­е­ся в одной цифре на еди­ни­цу (если на­зван­ное число со­дер­жит цифру 0 или 9, не­ко­то­рые клет­ки кре­сти­ка вы­хо­дят за края пря­мо­уголь­ни­ка; таким клет­кам ни­ка­кие числа не со­от­вет­ству­ют). За­да­ча Гриши  — по­крыть пря­мо­уголь­ник 9 × 10 та­ки­ми кре­сти­ка­ми. Убе­дим­ся, что 18 кре­сти­ков ему не хва­тит. Сум­мар­ная пло­щадь кре­сти­ков равна 18 × 5  =  90, т. е. равна пло­ща­ди пря­мо­уголь­ни­ка. Но, по­кры­вая уг­ло­вую клет­ку, мы не­из­беж­но вый­дем за пре­де­лы пря­мо­уголь­ни­ка, и эта по­те­ря по­ме­ша­ет по­крыть весь пря­мо­уголь­ник.

б, в)  Решим сразу пункт в)  — убе­дим­ся, что 22 по­пы­ток хва­тит. По­кры­тие из 22 кре­сти­ков легко найти, если за­ме­тить, что кре­сти­ка­ми можно вы­ло­жить плос­кость без пе­ре­кры­тий (прав­да, придётся ещё до­ба­вить не­сколь­ко кре­сти­ков по краям пря­мо­уголь­ни­ка). На­при­мер, Гриша может на­звать числа 11, 13, 17, 25, 29, 30, 32, 37, 44, 49, 51, 56, 63, 68, 70, 75, 82, 87, 89, 90, 94, 97.

При­ме­ча­ние Алек­сандра Ива­но­ва.

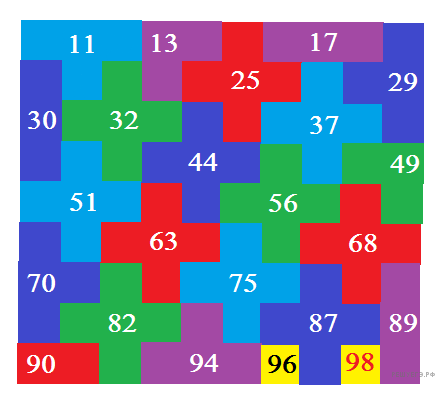
Да­вай­те рас­смот­рим пред­ло­жен­ную кар­тин­ку. Пря­мо­уголь­ник за­мо­щен фи­гу­ра­ми раз­ной формы: крест (5 кле­ток), Т-⁠об­раз­ный (4 клет­ки), трех­кле­точ­ные (уг­ло­вые и пря­мые), двух­кле­точ­ные фи­гу­ры и две оди­ноч­ные клет­ки.

Услы­шав «хо­лод­но», мы (Гриша) сразу от­бра­сы­ва­ем все клет­ки на­зван­ной фи­гу­ры, услы­шав «тепло»,  — на­чи­на­ем про­ве­рять. Для про­вер­ки раз­ных фигур тре­бу­ет­ся раз­ное мак­си­маль­ное ко­ли­че­ство до­пол­ни­тель­ных ходов: для кре­ста  — 3 хода, для Т-⁠об­раз­но­го и трех­кле­точ­ных фигур  — 2 хода, для двух­кле­точ­ных  — 1 ход.

Стра­те­гия со­сто­ит в сле­ду­ю­щем.

Сна­ча­ла на­зы­ва­ем числа, со­от­вет­ству­ю­щие кре­стам, по­сколь­ку для них тре­бу­ет­ся боль­ше про­ве­роч­ных ходов: 25, 32, 37, 44, 51, 56, 63, 68, 75, 82, 87 (всего 11 чисел). Если мы услы­ша­ли «тепло», то для уга­ды­ва­ния числа нам по­тре­бо­ва­лось мак­си­мум 11 + 3  =  14 ходов, если же всё время мы слы­ша­ли «хо­лод­но», то мы по­тра­ти­ли 11 ходов и ис­клю­чи­ли 55 чисел.

Далее на­зы­ва­ем числа, со­от­вет­ству­ю­щие Т-⁠об­раз­ным и трех­кле­точ­ным: 11, 13, 17, 29, 30, 49, 70, 89, 94 (таких чисел 9). Если мы те­перь услы­ша­ли «тепло», то для уга­ды­ва­ния числа нам по­тре­бо­ва­лось мак­си­мум 11 + 9 + 2  =  22 хода (Ура!!!), если же всё время мы и те­перь слы­ша­ли «хо­лод­но», то мы по­тра­ти­ли 11 + 9  =  20 ходов и ис­клю­чи­ли 55 + 31  =  86 чисел.

Далее на­зы­ва­ем число 90, это был два­дцать пер­вый ход. Если слы­шим «тепло», то про­ве­ря­ем одним ходом и от­га­ды­ва­ем число за 21 + 1  =  22 хода (Ура!!!), а если слы­шим «хо­лод­но», то вы­чер­ки­ва­ем еще 2 числа. Итого вы­черк­ну­то 86 + 2  =  88 чисел, за 21 ход. Оста­лось два не­вы­черк­ну­тых числа.

ФИНАЛ (по­след­ний, 22-⁠й ход): на­зы­ва­ем число 96. Если «тепло», то за­га­да­но число 96, если «хо­лод­но», то за­га­да­но число  98. УРА!!!

Таким об­ра­зом, Гриша (с нашей по­мо­щью), при пра­виль­ной стра­те­гии мак­си­мум за 22 хода обя­за­тель­но от­га­да­ет за­ду­ман­ное Лёшей дву­знач­ное число.