Найдите все значения a, при каждом из которых уравнение
имеет ровно один корень на отрезке [4; 8].
Решение. Уравнение равносильно следующей системе:
Рассмотрим первый случай, когда корни совпадают: 
Тогда корень 
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ.
Рассмотрим второй случай, когда первый корень 
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
Рассмотрим второй случай, когда второй корень 
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
Приведем другое решение:
Уравнение равносильно следующей системе:
В плоскости xOa графиком системы (а значит, и графиком исходного уравнения) будут отрезки прямых 
и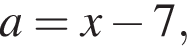 
лежащие внутри круга, ограниченного окружностью 
Решение системы на отрезке [4; 8] на рисунке изображено синим цветом.
Найдём значения параметра a (значения ординаты), при которых уравнение имеет единственное решение на отрезке [4; 8].
Для этого найдём ординату точки пересечения прямых и 
Ординаты точек пересечения прямой и окружности 
найдём, подставив в уравнение окружности 
Таким образом, исходное уравнение имеет на отрезке [4; 8] ровно один корень при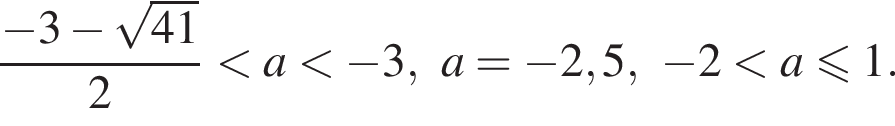 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений а. | 2 |
| Верно получена хотя бы одна граничная точка искомого множества значений а. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |