Целое число S является суммой не менее трех последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел.
а) Может ли S равняться 8?
б) Может ли S равняться 1?
в) Найдите все значения, которые может принимать S.
Решение. а) Число 8 является суммой четырех последовательных членов арифметической прогрессии. Например, 8 = − 1 + 1 + 3 + 5.
б) Пусть число 1 является суммой первых k членов арифметической прогрессии с первым членом а и разностью d. Тогда
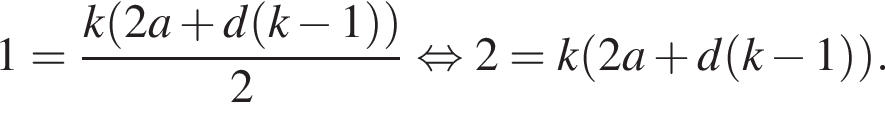
Значит, число k — делитель 2, что противоречит условию 
в) Любое натурально число 
является суммой арифметической прогрессии 
состоящей из 
членов. Если заменить все члены этой прогрессии на противоположные, то получится арифметическая прогрессия, состоящая из 2n членов, сумма которой равна −n.
В предыдущем пункте мы показали, что S не может равняться 1. Аналогично можно показать, что S не может равняться −1. Число S может равняться 0, например, для прогрессии −1; 0; 1. Таким образом, S может принимать любые целые значения, кроме −1 и 1.
Ответ: а) да; б) нет; в) любые целые значения, кроме −1 и 1.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующий результатов: ― пример в п. а; ― обоснованное решение в п. б; ― обоснование в п. в того, что S может принимать все целые значения (отличные от −1 и 1); ― обоснование в п. в того, что равенства S = −1 и S = 1 невозможны | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |