Тип 18 № 502098 
Источники:
Классификатор алгебры: Уравнения с параметром, Уравнения смешанного типа
Методы алгебры: Перебор случаев, Перебор случаев
Задача с параметром. Аналитическое решение уравнений и неравенств
i
Найдите все значения a, при которых уравнение 
имеет на промежутке 
единственный корень.
Решение. Первый случай: 
Тогда
Последнее уравнение имеет на промежутке 
единственный корень при 
откуда 
Подставив 
в неравенство 
получим:
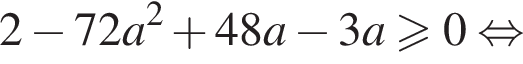
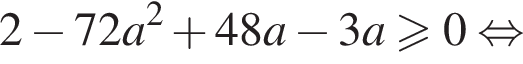
В этом случае уравнение при условии 
имеет на промежутке единственный корень 
при 
и не имеет на промежутке корней при 
и при 
Второй случай: 
Тогда из исходного уравнения получаем:
Последнее уравнение имеет на промежутке единственный корень 
Подставив 
в неравенство 
получим: 
откуда 
В этом случае уравнение 
при условии имеет на промежутке единственный корень 
при 
и не имеет на промежутке корней при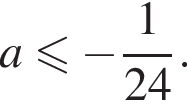 
Ответ: 
Критерии проверки:
| Критерии оценивания ответа на задание С5 | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
502098
Классификатор алгебры: Уравнения с параметром, Уравнения смешанного типа
Методы алгебры: Перебор случаев, Перебор случаев