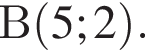Найдите все целочисленные значения параметра а, при каждом из которых система
имеет единственное решение.
Решение. Пусть (x, y) — решение системы. Тогда при любом значении параметра a левая часть первого уравнения системы есть сумма расстояний от точки (x, y) до точек (1, a) и (5, a), лежащих на прямой y = a , параллельной оси абсцисс. Но расстояние между точками (1, a) и (5, a) равно 4, и поэтому решение первого уравнения — множество точек (x, y), причём 1 ≤ x ≤ 5, y = a, поскольку иначе
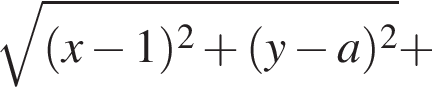
Следовательно, данная система имеет единственное решение тогда и только тогда, когда второе уравнение системы имеет единственное решение на отрезке 1 ≤ x ≤ 5.
Рассмотрим квадратичную функцию
Её график — парабола, направленная ветвями вверх. Поскольку свободный 
при любом a, то корни этой функции имеют разные знаки. В этом случае единственный положительный корень функции 
лежит на отрезке 1 ≤ x ≤ 5 тогда и только тогда, когда 
и 
Получаем систему:
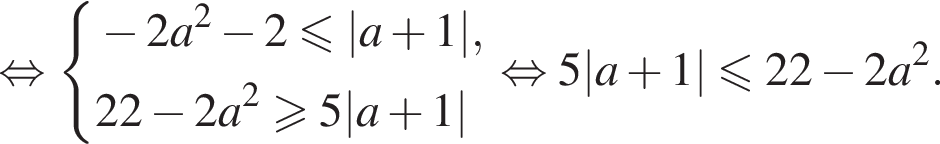
Поскольку любое решение полученного неравенства должно удовлетворять условию 
то есть 
и по условию a — целое число, то решениями неравенства могут быть только 
Из этих условий проверкой получаем все решения: −2, ±1, 0.
Ответ: −2, ±1, 0.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 4 |
| С помощью верного рассуждения получены все значения a, но ответ содержит лишнее значение. | 3 |
| С помощью верного рассуждения получены одно или несколько значений a | 2 |
| Задача верно сведена к исследованию взаимного расположения корней квадратичной функции (аналитически или графически). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |
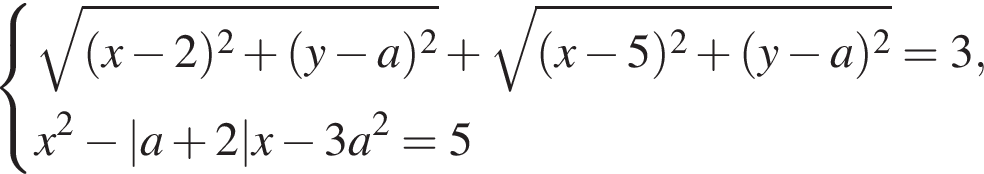
при любом a, то корни этой функции имеют разные знаки. Известно, что в этом случае единственный положительный корень функции 
лежит на отрезке 2 ≤ x ≤ 5 тогда и только тогда, когда 
и 
то есть 
и по условию a — целое число, то решениями неравенства могут быть только 
Из этих условий проверкой получаем все решения: −2, ±1, 0.
до точек 
и 
равно 
Поскольку расстояние между точками 
это означает, что точка 
Другими словами, она удовлетворяет уравнению 
и условию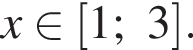 
возрастающая (как сумма двух возрастающих), каждое значение она принимает ровно один раз. Поэтому решение 
— единственное, ему соответствует 
то 
при остальных а нет решений.
которые лежат на отрезке AB прямой, соединяющей точки 
и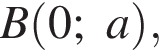 
поскольку уравнение задаёт множество точек 
сумма расстояний от каждой из которых до точек А и В равна 
что равно длине отрезка АВ.
параллельной оси абсцисс и проходящей через точку 
Если 
то точки В и О совпадают, и система не имеет решений. Для 
условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой O или с точкой В, то условие задачи выполнено.
Имеем:
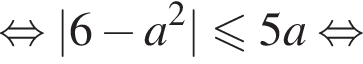
может пересекать отрезок АB только в точке А. Тогда 
единственным отрицательным корнем этого уравнения является 
означает, что сумма расстояний от точки 
до точек 
и 
равна 
но эта сумма расстояний всегда больше, чем 
Значит, множество решений при 
— это отрезок с концами 
множество решений — это 
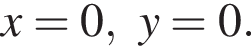
— круг на плоскости с координатами 
Отсюда получаем необходимое условие существование единственного решения — отрезок с концами 
В случае касания это расстояние должно совпадать с радиусом круга, откуда получаем уравнение 
Таким образом, система имеет единственное решение при 
и 
, но ответ содержит лишнее значение.
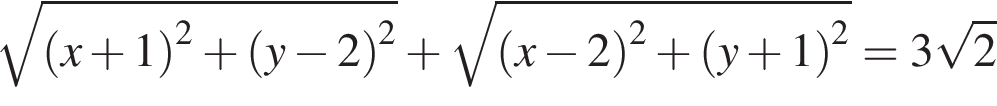
т. е. множество точек отрезка AB.
и 
проходят соответственно через точки 
и 
либо значение 
где a3 ― то значения параметра а, при котором прямая AB, задаваемая уравнением 
касается графика уравнения 
при 
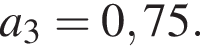
и это значит, что точка M лежит на отрезке AB. В нашем случае точки А и В имеют координаты: 
Расстояние между этими точками равно 4. Действительно, рассматриваемое уравнение задает отрезок AB. 
и полуокружностью 
c центром в точке 
и радиусом, равным 2.
и 
Решения первого уравнения: 
Решения второго уравнения: 
где k и n — целые. Следовательно, уравнения 
система имеет наибольшее число решений, а именно 5. Они соответствуют точкам 
и 
всего 9 пар. Наконец из уравнения (2) следует, что решение принадлежит отрезку с концами в точках 
и 
При 
число решений окажется максимальным.