Решите неравенство 
Решение. Преобразуем неравенство:
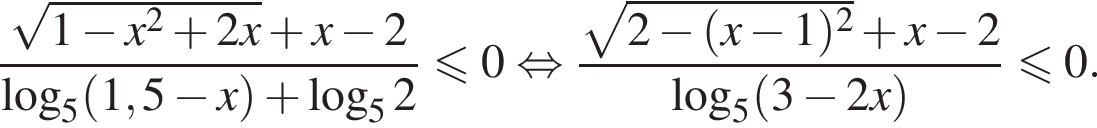
Решим неравенство методом интервалов.
1. Найдём ОДЗ:
2. Найдём значения x, при которых числитель левой части обращается в нуль:
3. Отметим на числовой оси ОДЗ неравенства и найденный корень, методом пробных точек определим знаки выражения на каждом из получившихся промежутков.
При 
получаем:
поскольку числитель положителен, а знаменатель отрицателен.
При 
получаем:
поскольку числитель и знаменатель положительны.
При 
получаем:
поскольку числитель отрицателен, а знаменатель положителен.
Расставим найденные знаки на числовой оси:
Таким образом, 
или 
Ответ: 
Примечание.
Число является границей ОДЗ, но не обращает левую часть неравенства в нуль, поэтому его можно использовать для определения знака левой части на промежутке 
Приведём другое решение.
Воспользуемся методом рационализации:
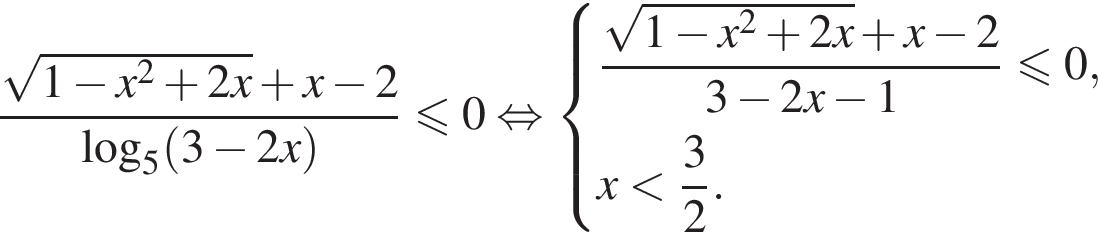
При 
верно равенство 
Тогда получим
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |