i
На окружности отмечены точки K, L, M, N, причем прямые KL и MN пересекаются вне круга в точке E, прямые LM и KN пересекаются вне круга в точке F. Биссектриса угла KEN пересекает отрезки LM и KN в точках P и R соответственно. Прямая, проведенная через точку F перпендикулярно прямой PR, пересекает отрезки KL и MN в точках S и Q соответственно.
а) Докажите, что PQRS — ромб.
б) Найдите площадь четырехугольника PQRS, если известно, что EL = 4, EM = 6, LM = 5 и KN = 15.
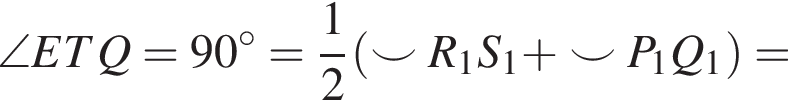
значит, треугольник RFP — равнобедренный и RT = TP. Аналогично ST = TQ, тогда четырёхугольник PQRS — параллелограмм с перпендикулярными диагоналями, то есть ромб.
тогда треугольники KEN и MEL подобны по двум углам, значит, 
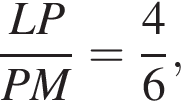тогда LP = 2 и PM = 3. Аналогично треугольники FNM и FLK подобны, следовательно, 
откуда NQ = 2,4 и QM = 3,6. 
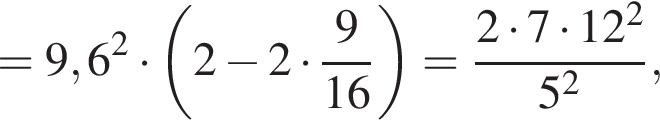
Аналогично 
