РЕШУ ЕГЭ — математика профильная

Задания

Тип 15 № 640281 Добавить в вариант

Источник: А. Ларин. Тренировочный вариант № 426

Классификатор алгебры: Неравенства с логарифмами по переменному основанию

Методы алгебры: Введение замены, Метод интервалов

Неравенства. Неравенства с логарифмами по переменному основанию

Решите неравенство: 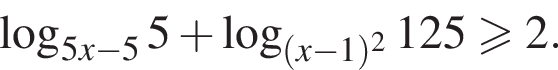$логарифм по основанию левая круглая скобка 5 x минус 5 правая круглая скобка 5 плюс логарифм по основанию левая круглая скобка левая круглая скобка x минус 1 правая круглая скобка в квадрате правая круглая скобка 125 больше или равно 2.$

Решение. Перейдём в левой части неравенства к логарифмам по основанию 5:

$дробь: числитель: логарифм по основанию 5 5, знаменатель: логарифм по основанию 5 левая круглая скобка 5x минус 5 правая круглая скобка конец дроби плюс дробь: числитель: логарифм по основанию 5 125, знаменатель: логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка в квадрате конец дроби =$
$= дробь: числитель: 1, знаменатель: логарифм по основанию 5 левая круглая скобка 5 левая круглая скобка x минус 1 правая круглая скобка правая круглая скобка конец дроби плюс дробь: числитель: 3, знаменатель: логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка в квадрате конец дроби =$
$= дробь: числитель: 1, знаменатель: логарифм по основанию 5 5 плюс логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка конец дроби плюс дробь: числитель: 3, знаменатель: 2 логарифм по основанию 5 |x минус 1| конец дроби .$

В знаменателе первой дроби стоит выражение $логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка ,$ которое определено лишь при $x минус 1 больше 0.$ При этом условии раскроем модуль в знаменателе второй дроби, получим:

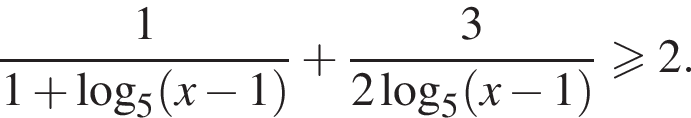
$дробь: числитель: 1, знаменатель: 1 плюс логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка конец дроби плюс дробь: числитель: 3, знаменатель: 2 логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка конец дроби больше или равно 2.$

Пусть $логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка =t,$ тогда

$дробь: числитель: 1, знаменатель: 1 плюс t конец дроби плюс дробь: числитель: 3, знаменатель: 2t конец дроби больше или равно 2 равносильно дробь: числитель: 2t плюс 3 левая круглая скобка 1 плюс t правая круглая скобка минус 4t левая круглая скобка t плюс 1 правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно$
$равносильно дробь: числитель: минус 4t в квадрате плюс t плюс 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно дробь: числитель: 4t в квадрате минус t минус 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно$
$равносильно дробь: числитель: 4 левая круглая скобка t минус 1 правая круглая скобка левая круглая скобка t плюс дробь: числитель: 3, знаменатель: 4 конец дроби правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно совокупность выражений минус 1 меньше t меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше t меньше или равно 1. конец совокупности .$ $дробь: числитель: 1, знаменатель: 1 плюс t конец дроби плюс дробь: числитель: 3, знаменатель: 2t конец дроби больше или равно 2 равносильно$
$равносильно дробь: числитель: 2t плюс 3 левая круглая скобка 1 плюс t правая круглая скобка минус 4t левая круглая скобка t плюс 1 правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно$
$равносильно дробь: числитель: минус 4t в квадрате плюс t плюс 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно дробь: числитель: 4t в квадрате минус t минус 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно$
$равносильно дробь: числитель: 4 левая круглая скобка t минус 1 правая круглая скобка левая круглая скобка t плюс дробь: числитель: 3, знаменатель: 4 конец дроби правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно совокупность выражений минус 1 меньше t меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше t меньше или равно 1. конец совокупности .$ $дробь: числитель: 1, знаменатель: 1 плюс t конец дроби плюс дробь: числитель: 3, знаменатель: 2t конец дроби больше или равно 2 равносильно$
$равносильно дробь: числитель: 2t плюс 3 левая круглая скобка 1 плюс t правая круглая скобка минус 4t левая круглая скобка t плюс 1 правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно$
$равносильно дробь: числитель: минус 4t в квадрате плюс t плюс 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби больше или равно 0 равносильно$
$равносильно дробь: числитель: 4t в квадрате минус t минус 3, знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно$
$равносильно дробь: числитель: 4 левая круглая скобка t минус 1 правая круглая скобка левая круглая скобка t плюс дробь: числитель: 3, знаменатель: 4 конец дроби правая круглая скобка , знаменатель: 2t левая круглая скобка 1 плюс t правая круглая скобка конец дроби меньше или равно 0 равносильно$
$равносильно совокупность выражений минус 1 меньше t меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше t меньше или равно 1. конец совокупности .$

Вернёмся к исходной переменной:

$совокупность выражений минус 1 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно 1. конец совокупности . равносильно совокупность выражений 5 в степени левая круглая скобка минус 1 правая круглая скобка меньше x минус 1 меньше или равно 5 в степени левая круглая скобка минус \tfrac34 правая круглая скобка ,5 в степени 0 меньше x минус 1 меньше или равно 5 в степени 1 конец совокупности . равносильно$
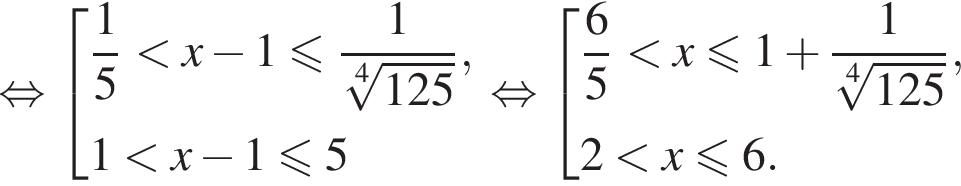
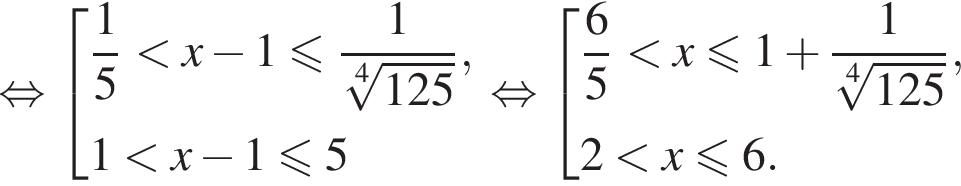
$равносильно совокупность выражений дробь: числитель: 1, знаменатель: 5 конец дроби меньше x минус 1 меньше или равно дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,1 меньше x минус 1 меньше или равно 5 конец совокупности . равносильно совокупность выражений дробь: числитель: 6, знаменатель: 5 конец дроби меньше x меньше или равно 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,2 меньше x меньше или равно 6. конец совокупности .$ $совокупность выражений минус 1 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно 1. конец совокупности . равносильно$
$равносильно совокупность выражений 5 в степени левая круглая скобка минус 1 правая круглая скобка меньше x минус 1 меньше или равно 5 в степени левая круглая скобка минус \tfrac34 правая круглая скобка ,5 в степени 0 меньше x минус 1 меньше или равно 5 в степени 1 конец совокупности . равносильно$
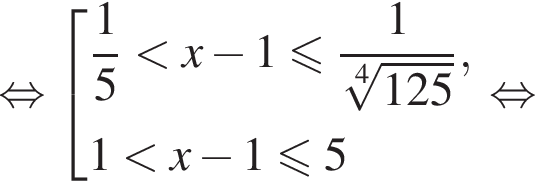
$равносильно совокупность выражений дробь: числитель: 1, знаменатель: 5 конец дроби меньше x минус 1 меньше или равно дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,1 меньше x минус 1 меньше или равно 5 конец совокупности . равносильно совокупность выражений дробь: числитель: 6, знаменатель: 5 конец дроби меньше x меньше или равно 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,2 меньше x меньше или равно 6. конец совокупности .$ $совокупность выражений минус 1 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно минус дробь: числитель: 3, знаменатель: 4 конец дроби ,0 меньше логарифм по основанию 5 левая круглая скобка x минус 1 правая круглая скобка меньше или равно 1. конец совокупности . равносильно$
$равносильно совокупность выражений 5 в степени левая круглая скобка минус 1 правая круглая скобка меньше x минус 1 меньше или равно 5 в степени левая круглая скобка минус \tfrac34 правая круглая скобка ,5 в степени 0 меньше x минус 1 меньше или равно 5 в степени 1 конец совокупности . равносильно$
$равносильно совокупность выражений дробь: числитель: 1, знаменатель: 5 конец дроби меньше x минус 1 меньше или равно дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,1 меньше x минус 1 меньше или равно 5 конец совокупности . равносильно$
$равносильно совокупность выражений дробь: числитель: 6, знаменатель: 5 конец дроби меньше x меньше или равно 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби ,2 меньше x меньше или равно 6. конец совокупности .$

Ответ: $левая круглая скобка дробь: числитель: 6, знаменатель: 5 конец дроби ; 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби правая квадратная скобка \cup левая круглая скобка 2; 6 правая квадратная скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

640281

$левая круглая скобка дробь: числитель: 6, знаменатель: 5 конец дроби ; 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби правая квадратная скобка \cup левая круглая скобка 2; 6 правая квадратная скобка .$

Источник: А. Ларин. Тренировочный вариант № 426

Классификатор алгебры: Неравенства с логарифмами по переменному основанию

Методы алгебры: Введение замены, Метод интервалов

Ключ

№ п/п	№ задания	Ответ
1	640281	$левая круглая скобка дробь: числитель: 6, знаменатель: 5 конец дроби ; 1 плюс дробь: числитель: 1, знаменатель: корень 4 степени из: начало аргумента: 125 конец аргумента конец дроби правая квадратная скобка \cup левая круглая скобка 2; 6 правая квадратная скобка .$