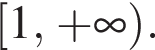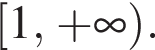Найдите все значения параметра a, при каждом из которых уравнение
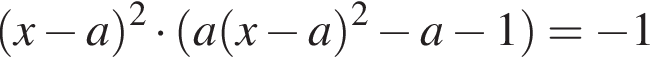
имеет больше положительных корней, чем отрицательных.
Решение. Пусть  тогда
тогда

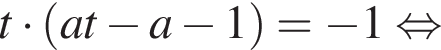

При ![]() получаем
получаем ![]() откуда находим:
откуда находим:
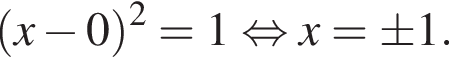
Положительных и отрицательных корней поровну, условие задачи не выполнено.
При ![]() имеем:
имеем:





Вернёмся к исходной переменной, получим совокупность уравнений:

или

При ![]() второе уравнение совокупности корней не имеет, а у первого уравнения два корня, среди которых не менее одного отрицательного (см. рис. 1). Значит, при
второе уравнение совокупности корней не имеет, а у первого уравнения два корня, среди которых не менее одного отрицательного (см. рис. 1). Значит, при ![]() условие задачи не выполнено.
условие задачи не выполнено.
![]()
![]()
При ![]() каждое уравнение совокупности имеет два корня, среди которых не менее одного положительного (см. рис. 2). Значит, для выполнения условия задачи необходимо и достаточно чтобы хотя бы одно из двух уравнений не имело отрицательного корня, то есть выполнялась совокупность условий
каждое уравнение совокупности имеет два корня, среди которых не менее одного положительного (см. рис. 2). Значит, для выполнения условия задачи необходимо и достаточно чтобы хотя бы одно из двух уравнений не имело отрицательного корня, то есть выполнялась совокупность условий

Таким образом, условие задачи выполняется при ![]()
Ответ: 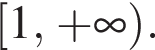
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены верные значения параметра, но допущен недочет | 3 |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения, ИЛИ в решении верно найдены все граничные точки множества значений параметра, но неверно определены промежутки значений | 2 |
| В случае аналитического решения: задача верно сведена к набору решенных уравнений и неравенств с учетом требуемых ограничений, ИЛИ в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |