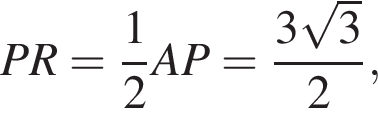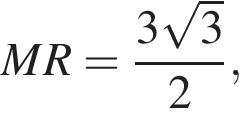i
Основанием правильной треугольной пирамиды MABC является треугольник ABC со стороной 6. Ребро MA перпендикулярно грани MBC. Через вершину пирамиды M и середины ребер
а) Докажите, что сечение пирамиды плоскостью α является равносторонним треугольником.
б) Найдите расстояние от вершины C до плоскости α.
и, следовательно, 
Отрезок ML в нём является медианой из вершины прямого угла, следовательно, 
Аналогично, из равенства боковых граней, следует, что MK = 3, следовательно, треугольник KLM — равносторонний.
и 
а значит, прямые PG и CH перпендикулярны плоскости KLM и CH является искомым расстоянием. При этом R — середина CP и прямоугольные треугольники PRG и CRH равны. Имеем:
