РЕШУ ЕГЭ — математика профильная

Задания

Тип 15 № 562040 Добавить в вариант

Источник: Избранные задания по математике из последних сборников ФИПИ

Классификатор алгебры: Логарифмические неравенства, Неравенства первой и второй степени относительно логарифмической функции, Неравенства смешанного типа, Область определения неравенства, Показательные уравнения и неравенства

Методы алгебры: Замена переменной, Метод интервалов

Неравенства. Логарифмы и показательные выражения

Решите неравенство $левая круглая скобка 2 умножить на 0,5 в степени левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 умножить на 2 в степени левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка \times$
$\times левая круглая скобка 2\log в квадрате _0,5 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка \leqslant0.$

Решение. Преобразуем неравенство:

$левая круглая скобка 2 умножить на 0,5 в степени левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 умножить на 2 в степени левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка левая круглая скобка 2\log в квадрате _0,5 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка \leqslant0 равносильно$

$равносильно левая круглая скобка 2 умножить на 2 в степени левая круглая скобка минус x минус 2 правая круглая скобка минус 0,5 умножить на 2 в степени левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка левая круглая скобка 2\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка меньше или равно 0 равносильно$

$равносильно левая круглая скобка 2 в степени левая круглая скобка минус x минус 1 правая круглая скобка минус 2 в степени левая круглая скобка x плюс 1 правая круглая скобка правая круглая скобка левая круглая скобка 2\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка правая круглая скобка меньше или равно 0.$

Найдем нули первого сомножителя:

$2 в степени левая круглая скобка минус x минус 1 правая круглая скобка = 2 в степени левая круглая скобка x плюс 1 правая круглая скобка равносильно минус x минус 1 = x плюс 1 равносильно x = минус 1.$ $2 в степени левая круглая скобка минус x минус 1 правая круглая скобка = 2 в степени левая круглая скобка x плюс 1 правая круглая скобка равносильно$
$равносильно минус x минус 1 = x плюс 1 равносильно x = минус 1.$

Найденный корень лежит в ОДЗ логарифма.

Найдем нули второго сомножителя:

$2\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно 4\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка левая круглая скобка 4 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка минус 1 правая круглая скобка = 0 равносильно$
$равносильно совокупность выражений логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0, логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = дробь: числитель: 1, знаменатель: 4 конец дроби конец совокупности . равносильно совокупность выражений x плюс 2 = 1,x плюс 2 = корень 4 степени из: начало аргумента: 2 конец аргумента конец совокупности . равносильно совокупность выражений x = минус 1,x = корень 4 степени из: начало аргумента: 2 конец аргумента минус 2. конец совокупности .$ $2\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно 4\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка левая круглая скобка 4 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка минус 1 правая круглая скобка = 0 равносильно$
$равносильно совокупность выражений логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0, логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = дробь: числитель: 1, знаменатель: 4 конец дроби конец совокупности . равносильно$
$равносильно совокупность выражений x плюс 2 = 1,x плюс 2 = корень 4 степени из: начало аргумента: 2 конец аргумента конец совокупности . равносильно совокупность выражений x = минус 1,x = корень 4 степени из: начало аргумента: 2 конец аргумента минус 2. конец совокупности .$ $2\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус 0,5 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно 4\log в квадрате _2 левая круглая скобка x плюс 2 правая круглая скобка минус логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0 равносильно$
$равносильно логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка левая круглая скобка 4 логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка минус 1 правая круглая скобка = 0 равносильно$
$равносильно совокупность выражений логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = 0, логарифм по основанию 2 левая круглая скобка x плюс 2 правая круглая скобка = дробь: числитель: 1, знаменатель: 4 конец дроби конец совокупности . равносильно$
$равносильно совокупность выражений x плюс 2 = 1,x плюс 2 = корень 4 степени из: начало аргумента: 2 конец аргумента конец совокупности . равносильно$
$равносильно совокупность выражений x = минус 1,x = корень 4 степени из: начало аргумента: 2 конец аргумента минус 2. конец совокупности .$

Сравним полученные числа:

$минус 1 меньше корень 4 степени из: начало аргумента: 2 конец аргумента минус 2 равносильно 1 меньше корень 4 степени из: начало аргумента: 2 конец аргумента равносильно 1 меньше 2,$

поэтому число −1 на числовой оси лежит левее числа $корень 4 степени из: начало аргумента: 2 конец аргумента минус 2.$

Применим метод интервалов на ОДЗ неравенства, получим: 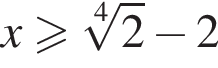$x больше или равно корень 4 степени из: начало аргумента: 2 конец аргумента минус 2$ или $x = минус 1.$

Ответ: $левая фигурная скобка минус 1 правая фигурная скобка \cup левая квадратная скобка корень 4 степени из: начало аргумента: 2 конец аргумента минус 2; плюс бесконечность правая круглая скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

562040

$левая фигурная скобка минус 1 правая фигурная скобка \cup левая квадратная скобка корень 4 степени из: начало аргумента: 2 конец аргумента минус 2; плюс бесконечность правая круглая скобка .$

Источник: Избранные задания по математике из последних сборников ФИПИ

Методы алгебры: Замена переменной, Метод интервалов

Ключ

№ п/п	№ задания	Ответ
1	562040	$левая фигурная скобка минус 1 правая фигурная скобка \cup левая квадратная скобка корень 4 степени из: начало аргумента: 2 конец аргумента минус 2; плюс бесконечность правая круглая скобка .$