РЕШУ ЕГЭ — математика профильная

Задания

Тип 15 № 550263 Добавить в вариант

Источник: А. Ларин. Тренировочный вариант № 323. (часть C)

Классификатор алгебры: Иррациональные неравенства, Неравенства смешанного типа, Область определения неравенства, Показательные уравнения и неравенства, Сравнение чисел

Методы алгебры: Метод интервалов

Неравенства. Показательные выражения и иррациональности

Решите неравенство $корень из: начало аргумента: 4 в степени x минус 5 умножить на 2 в степени левая круглая скобка x плюс 1 конец аргумента плюс 25 правая круглая скобка плюс корень из: начало аргумента: 9 в степени x минус 2 умножить на 3 в степени левая круглая скобка x плюс 2 конец аргумента плюс 17 правая круглая скобка меньше или равно 2 в степени x минус 5.$

Решение. Преобразуем неравенство:

$корень из: начало аргумента: 4 в степени x минус 5 умножить на 2 в степени левая круглая скобка x плюс 1 конец аргумента плюс 25 правая круглая скобка плюс корень из: начало аргумента: 9 в степени x минус 2 умножить на 3 в степени левая круглая скобка x плюс 2 конец аргумента плюс 17 правая круглая скобка меньше или равно 2 в степени x минус 5 равносильно$
$равносильно корень из: начало аргумента: 4 в степени x минус 10 умножить на 2 в степени x плюс 25 конец аргумента плюс корень из: начало аргумента: 9 в степени x минус 18 умножить на 3 в степени x плюс 17 конец аргумента меньше или равно 2 в степени x минус 5 равносильно$

$равносильно корень из: начало аргумента: левая круглая скобка 2 в степени x минус 5 правая круглая скобка в квадрате конец аргумента плюс корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента меньше или равно 2 в степени x минус 5 равносильно$
$равносильно \left|2 в степени x минус 5| плюс корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента меньше или равно 2 в степени x минус 5.$

Заметим, что при $2 в степени x минус 5 меньше 0$ левая часть неравенства неотрицательна, а правая  — отрицательна, значит, неравенство не имеет решений. Тогда $2 в степени x минус 5 больше или равно 0,$ а значит, $|2 в степени x минус 5| = 2 в степени x минус 5.$ Получаем:

$система выражений 2 в степени x минус 5 плюс корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента меньше или равно 2 в степени x минус 5,2 в степени x минус 5\geqslant0 конец системы . равносильно$
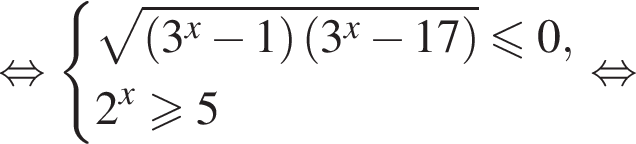
$равносильно система выражений корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента меньше или равно 0,2 в степени x \geqslant5 конец системы . равносильно$

$равносильно система выражений корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента = 0,2 в степени x \geqslant5 конец системы . равносильно система выражений совокупность выражений 3 в степени x =1,3 в степени x =17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно$
$равносильно система выражений совокупность выражений x=0,x= логарифм по основанию 3 17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно система выражений x= логарифм по основанию 3 17,x больше или равно логарифм по основанию 2 5. конец системы .$ $равносильно система выражений корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента = 0,2 в степени x \geqslant5 конец системы . равносильно$
$равносильно система выражений совокупность выражений 3 в степени x =1,3 в степени x =17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно$
$равносильно система выражений совокупность выражений x=0,x= логарифм по основанию 3 17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно система выражений x= логарифм по основанию 3 17,x больше или равно логарифм по основанию 2 5. конец системы .$ $равносильно система выражений корень из: начало аргумента: левая круглая скобка 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 17 правая круглая скобка конец аргумента = 0,2 в степени x \geqslant5 конец системы . равносильно$
$равносильно система выражений совокупность выражений 3 в степени x =1,3 в степени x =17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно$
$равносильно система выражений совокупность выражений x=0,x= логарифм по основанию 3 17, конец системы . 2 в степени x \geqslant5 конец совокупности . равносильно$
$равносильно система выражений x= логарифм по основанию 3 17,x больше или равно логарифм по основанию 2 5. конец системы .$

Сравним числа $логарифм по основанию 3 17$ и $логарифм по основанию 2 5$ :

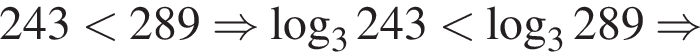
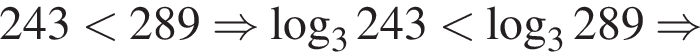
$243 меньше 289 \Rightarrow логарифм по основанию 3 243 меньше логарифм по основанию 3 289 \Rightarrow$
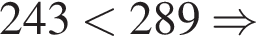
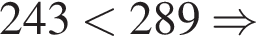
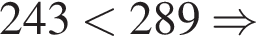
$\Rightarrow 5 меньше логарифм по основанию 3 17 в квадрате \Rightarrow 5 меньше 2 логарифм по основанию 3 17 \Rightarrow дробь: числитель: 5, знаменатель: 2 конец дроби меньше логарифм по основанию 3 17,$ $243 меньше 289 \Rightarrow логарифм по основанию 3 243 меньше логарифм по основанию 3 289 \Rightarrow$
$\Rightarrow 5 меньше логарифм по основанию 3 17 в квадрате \Rightarrow$
$\Rightarrow 5 меньше 2 логарифм по основанию 3 17 \Rightarrow дробь: числитель: 5, знаменатель: 2 конец дроби меньше логарифм по основанию 3 17,$ $243 меньше 289 \Rightarrow$
$\Rightarrow логарифм по основанию 3 243 меньше логарифм по основанию 3 289 \Rightarrow$
$\Rightarrow 5 меньше логарифм по основанию 3 17 в квадрате \Rightarrow 5 меньше 2 логарифм по основанию 3 17 \Rightarrow$
$\Rightarrow дробь: числитель: 5, знаменатель: 2 конец дроби меньше логарифм по основанию 3 17,$ $243 меньше 289 \Rightarrow$
$\Rightarrow логарифм по основанию 3 243 меньше логарифм по основанию 3 289 \Rightarrow$
$\Rightarrow 5 меньше логарифм по основанию 3 17 в квадрате \Rightarrow$
$\Rightarrow 5 меньше 2 логарифм по основанию 3 17 \Rightarrow дробь: числитель: 5, знаменатель: 2 конец дроби меньше логарифм по основанию 3 17,$ $243 меньше 289 \Rightarrow$
$\Rightarrow логарифм по основанию 3 243 меньше логарифм по основанию 3 289 \Rightarrow$
$\Rightarrow 5 меньше логарифм по основанию 3 17 в квадрате \Rightarrow$
$\Rightarrow 5 меньше 2 логарифм по основанию 3 17 \Rightarrow$
$\Rightarrow дробь: числитель: 5, знаменатель: 2 конец дроби меньше логарифм по основанию 3 17,$

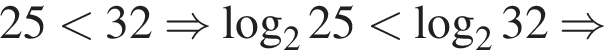
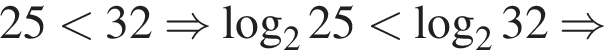
$25 меньше 32 \Rightarrow логарифм по основанию 2 25 меньше логарифм по основанию 2 32 \Rightarrow$
$\Rightarrow логарифм по основанию 2 5 в квадрате меньше 5 \Rightarrow 2 логарифм по основанию 2 5 меньше 5 \Rightarrow логарифм по основанию 2 5 меньше дробь: числитель: 5, знаменатель: 2 конец дроби .$ $25 меньше 32 \Rightarrow логарифм по основанию 2 25 меньше логарифм по основанию 2 32 \Rightarrow$
$\Rightarrow логарифм по основанию 2 5 в квадрате меньше 5 \Rightarrow$
$\Rightarrow 2 логарифм по основанию 2 5 меньше 5 \Rightarrow логарифм по основанию 2 5 меньше дробь: числитель: 5, знаменатель: 2 конец дроби .$ $25 меньше 32 \Rightarrow$
$\Rightarrow логарифм по основанию 2 25 меньше логарифм по основанию 2 32 \Rightarrow$
$\Rightarrow логарифм по основанию 2 5 в квадрате меньше 5 \Rightarrow$
$\Rightarrow 2 логарифм по основанию 2 5 меньше 5 \Rightarrow логарифм по основанию 2 5 меньше дробь: числитель: 5, знаменатель: 2 конец дроби .$

Значит, $логарифм по основанию 2 5 меньше логарифм по основанию 3 17,$ тогда

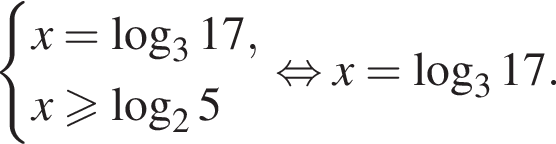
$система выражений x= логарифм по основанию 3 17,x больше или равно логарифм по основанию 2 5 конец системы . равносильно x= логарифм по основанию 3 17.$

Ответ: $левая фигурная скобка логарифм по основанию 3 17 правая фигурная скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Ответ: $левая фигурная скобка логарифм по основанию 3 17 правая фигурная скобка .$

550263

$левая фигурная скобка логарифм по основанию 3 17 правая фигурная скобка .$

Источник: А. Ларин. Тренировочный вариант № 323. (часть C)

Методы алгебры: Метод интервалов

Ключ

№ п/п	№ задания	Ответ
1	550263	$левая фигурная скобка логарифм по основанию 3 17 правая фигурная скобка .$