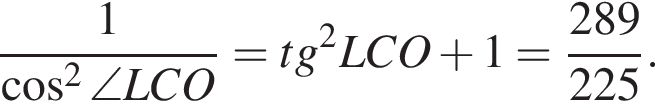i
В треугольной пирамиде SABC точка Е — середина ребра SA, точка F — середина ребра SB, О — точка пересечения медиан треугольника АВС.
а) Докажите, что плоскость CEF делит отрезок SO в отношении 3 : 2, считая от вершины S.
б) Найдите косинус угла между плоскостями CEF и EFT, если точка Т — середина SC, пирамида SABC правильная, площадь треугольника АВС равна ![]() а SB = 10.
а SB = 10.



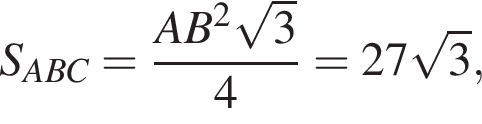
 а CO = 6.
а CO = 6.
 откуда
откуда