Ре­ше­ние. Пусть а вы­пла­ты с фев­ра­ля по июнь в 2030 и 2031 годах со­став­ля­ют по x тыс. руб. В июле 2027, 2028 и 2029 годов долг перед бан­ком не ме­ня­ет­ся, а еже­год­ные вы­пла­ты со­став­ля­ют по 220(k − 1) тыс. руб.

В ян­ва­ре 2030 года долг (в тыс. руб­лей) равен 220k, а в июле  — 220k − x. В ян­ва­ре 2031 года долг равен а в июле − По усло­вию, к июлю 2031 года долг будет вы­пла­чен пол­но­стью, зна­чит, от­ку­да

Таким об­ра­зом, общий раз­мер вы­плат со­став­ля­ет

от­ку­да Из по­лу­чен­но­го урав­не­ния на­хо­дим k  =  1,2, тогда r  =  20.

При­ве­дем дру­гое ре­ше­ние.

Обо­зна­чим сумму кре­ди­та за вы­пла­ту в пер­вые три года за a, а вы­пла­ту в по­след­ние два года за Тогда, если то   — так вы­гля­дит вы­пла­та в каж­дый из пер­вых трех годов. Усло­вие вы­пла­ты кре­ди­та двумя рав­ны­ми пла­те­жа­ми в по­след­ние два года да­ет­ся фор­му­лой Тогда

По усло­вию, сумма всех вы­плат со­став­ля­ет Под­став­ляя вы­ра­же­ния a и b, вы­ра­жен­ные через k, по­лу­ча­ем урав­не­ние:

Под­ста­вим имеем:

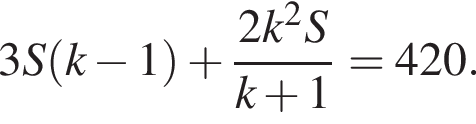
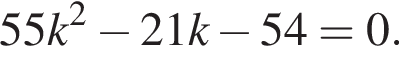от­ку­да по­лу­ча­ем квад­рат­ное урав­не­ние: В силу тео­ре­мы Виета, сумма кор­ней по­лу­чен­но­го урав­не­ния равна а их про­из­ве­де­ние равно Не­труд­но по­до­брать числа (см. ком­мен­та­рий ниже), удо­вле­тво­ря­ю­щие этим ра­вен­ствам: это числа и По тео­ре­ме, об­рат­ной тео­ре­ме Виета, най­ден­ные числа яв­ля­ют­ся кор­ня­ми этого квад­рат­но­го урав­не­ния. От­ри­ца­тель­ный ко­рень не под­хо­дит по смыс­лу за­да­чи. Тем самым от­ку­да

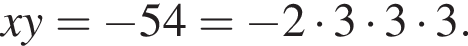Ком­мен­та­рий. Ис­хо­дя из про­из­ве­де­ния, ра­зум­но ис­кать корни в виде и где Кроме того, из суммы кор­ней на­хо­дим, что Те­перь под­би­ра­ем удо­вле­тво­ря­ю­щие си­сте­ме целые числа:

Ответ: 20.