Найдите все положительные значения параметра a, при которых система
имеет ровно три различных решения.
Решение. Заметим, что при x < 0 и при x > 4 левая часть первого уравнения системы не определена, а при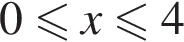 
первое уравнение системы принимает вид: 
или 
откуда 
При 
и a > 0 уравнение 
принимает вид 
откуда x = 0 или 
При и a > 0 уравнение 
принимает вид 
откуда 
или 
Для корня x = 0 условие 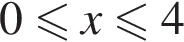выполнено. Для корня 
условие 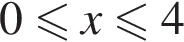выполнено при 
При положительных a корень отрицательный. Для корня 
условие 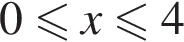при положительных a принимает вид:
Корни 
и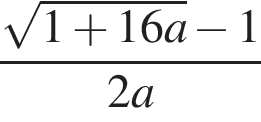 
не равны нулю при положительных a и совпадают при
Таким образом, исходная система уравнений имеет ровно три различных решения при 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом точек | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений а | 2 |
| Верно получена хотя бы одна граничная точка искомого множества значений а | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |