Найдите все значения параметра p, при каждом из которых система неравенств
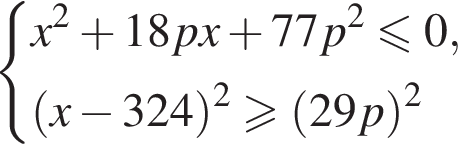
имеет единственное решение.
Решение. Преобразуем систему:
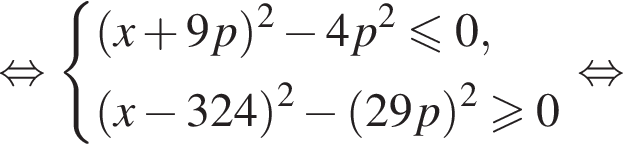
Изобразим решение системы в системе координат pOx. Множества точек, координаты которых являются решением каждого из неравенств, представляют собой пары вертикальных углов:
— для неравенства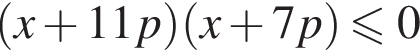 
это вертикальные углы, образованные прямыми 
и 
(см. рис., выделено синим);
— для неравенства 
это вертикальные углы, образованные прямыми 
и 
(выделено красным).
Пересечение этих областей (выделено сиреневым) соответствует решению системы.
Система имеет единственное решение, если 
или 
где 
— абсцисса точки пересечения прямых и 
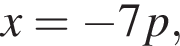а 
— абсцисса точки пересечения прямых и 
Найдём :
Найдём :
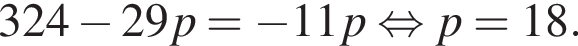
Таким образом, система имеет единственное решение, если 
или 
Ответ: 
Примечание.
Дополнительно заметим, что система не имеет решений, если 
или 
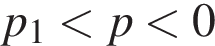система имеет бесконечно много решений, если 
или 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| С помощью верного рассуждения получен ответ, но в решении допущена вычислительная ошибка или оно недостаточно обосновано | 3 |
| С помощью верного рассуждения получен ответ, но в ходе решения допущена одна ошибка, отличная от вычислительной | 2 |
| Получены некоторые верные значения параметра, однако решение содержит более одной ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |