РЕШУ ЕГЭ — математика профильная

Задания

Тип Д15 C4 № 527608 Добавить в вариант

Источник: А. Ларин. Тренировочный вариант № 276

Сложная планиметрия. Комбинации фигур

Диагонали трапеции ABCD с основаниями AD и BC пересекаются в точке M. Окружность, описанная около треугольника CDM, пересекает отрезок AD в точке N и касается прямой BN.

а)  Докажите, что треугольники BNC и CDN подобны.

б)  Найдите AD, если $CD=24,$ $\angle BCD=\angle DMA,$ а радиус окружности равен 13.

Решение.

а)  Заметим, что $\angle BNM=\angle NDM$ (первый  — угол между касательной и хордой, второй  — вписанный угол) и $\angle MNC=\angle MDC$ (вписанные, опирающиеся на одну дугу). Значит,

$\angle BNC=\angle BNM плюс \angle MNC=\angle NDM плюс \angle CDM=\angle NDC.$ $\angle BNC=\angle BNM плюс \angle MNC=$
$=\angle NDM плюс \angle CDM=\angle NDC.$

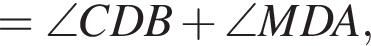
Кроме того из параллельности прямых AD и BC следует, что $\angle BCN=\angle CND,$ поэтому треугольники подобны по двум углам.

б)  Заметим, что

$\angle MAD плюс \angle ADM=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle AMD=$
$=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle BCD=\angle CDA=\angle CDB плюс \angle MDA,$ $\angle MAD плюс \angle ADM=$
$=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle AMD=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle BCD=$
$=\angle CDA=\angle CDB плюс \angle MDA,$ $\angle MAD плюс \angle ADM=$
$=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle AMD=$
$=180 в степени левая круглая скобка \circ правая круглая скобка минус \angle BCD=\angle CDA=$
$=\angle CDB плюс \angle MDA,$

откуда $\angle CAD=\angle CDB.$ Кроме того, $\angle BCA=\angle CAD$ из параллельности. Значит, $\angle CDM=\angle BCM,$ поэтому BC  — касательная к окружности. Тогда высота CH трапеции является частью диаметра окружности и, следовательно, проходит через середину хорды ND, откуда $CN=ND=24.$ Из теоремы синусов для треугольника CDN имеем $2 умножить на 13= дробь: числитель: 24, знаменатель: синус \angle CND конец дроби ,$ $синус \angle CND= дробь: числитель: 12, знаменатель: 13 конец дроби ,$ $косинус \angle CND= дробь: числитель: 5, знаменатель: 13 конец дроби ,$ $CH=CN умножить на синус \angle CND= дробь: числитель: 288, знаменатель: 13 конец дроби ,$ $NH= дробь: числитель: 120, знаменатель: 13 конец дроби ,$ $ND=2NH= дробь: числитель: 240, знаменатель: 13 конец дроби .$

Из пункта а) следует, что $BC:CN=CN:ND,$ откуда

$BC= дробь: числитель: CN в квадрате , знаменатель: ND конец дроби = дробь: числитель: 24 в квадрате умножить на 13, знаменатель: 240 конец дроби = дробь: числитель: 156, знаменатель: 5 конец дроби .$

Треугольники AMD и DCB подобны по двум углам, откуда $AD:BD=MD:BC,$ то есть

$дробь: числитель: 156, знаменатель: 5 конец дроби AD=BD умножить на MD=BD умножить на левая круглая скобка BD минус BM правая круглая скобка =$
$=BD в квадрате минус BD умножить на BM=BD в квадрате минус BC в квадрате =$ $дробь: числитель: 156, знаменатель: 5 конец дроби AD=BD умножить на MD=$
$=BD умножить на левая круглая скобка BD минус BM правая круглая скобка =$
$=BD в квадрате минус BD умножить на BM=BD в квадрате минус BC в квадрате =$ $дробь: числитель: 156, знаменатель: 5 конец дроби AD=BD умножить на MD=$
$=BD умножить на левая круглая скобка BD минус BM правая круглая скобка =$
$=BD в квадрате минус BD умножить на BM=$
$=BD в квадрате минус BC в квадрате =$

$= левая круглая скобка BC в квадрате плюс CD в квадрате минус 2BC умножить на CD умножить на косинус \angle BCD правая круглая скобка минус BC в квадрате =$
$= CD в квадрате минус 2BC умножить на CD умножить на косинус \angle BCD=$

$=CD в квадрате плюс 2BC умножить на CD умножить на косинус \angle CDA=$
$=24 в квадрате плюс 2 умножить на дробь: числитель: 156, знаменатель: 5 конец дроби умножить на 24 умножить на косинус \angle CND=$

$=24 в квадрате плюс 2 умножить на дробь: числитель: 156, знаменатель: 5 конец дроби умножить на 24 умножить на дробь: числитель: 5, знаменатель: 13 конец дроби =24 в квадрате плюс 2 умножить на 12 умножить на 24=48 умножить на 24.$ $=24 в квадрате плюс 2 умножить на дробь: числитель: 156, знаменатель: 5 конец дроби умножить на 24 умножить на дробь: числитель: 5, знаменатель: 13 конец дроби =$
$=24 в квадрате плюс 2 умножить на 12 умножить на 24=48 умножить на 24.$

Следовательно,

$AD=48 умножить на дробь: числитель: 24, знаменатель: \tfrac1565 конец дроби = дробь: числитель: 480, знаменатель: 13 конец дроби .$

Ответ: б) $дробь: числитель: 480, знаменатель: 13 конец дроби .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б	3
Получен обоснованный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

Ответ: б) $дробь: числитель: 480, знаменатель: 13 конец дроби .$

527608

б) $дробь: числитель: 480, знаменатель: 13 конец дроби .$

Источник: А. Ларин. Тренировочный вариант № 276

Ключ

№ п/п	№ задания	Ответ
1	527608	б) $дробь: числитель: 480, знаменатель: 13 конец дроби .$