i
В треугольнике ABC длина AB равна 3, 
хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. Известно, что 
площадь четырехугольника ABLM равна 2, а длина LM равна 1.
а) Найдите высоту треугольника KNC, опущенную из вершины C.
б) Найдите площадь треугольника KNC.
поэтому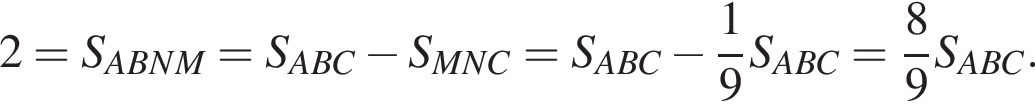 
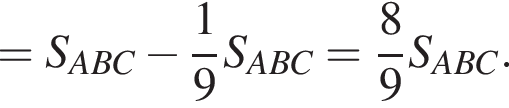
Обозначим стороны треугольника 
Тогда 
По теореме косинусов для треугольника ABC в то же время имеем 
поэтому 
и 
Значит, a и b являются корнями квадратного уравнения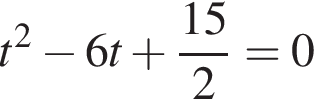 
(теорема Виета), поэтому они равны 
Будем считать, что 
тогда 
Из подобия, кроме того, 
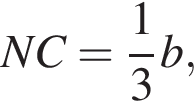
По свойству пересекающихся хорд имеем 
и 
Далее:
и 
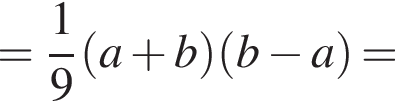
Прибавляя к этому уравнению удвоенное уравнение 
получим:
б) 