Найдите все a, при каждом из которых уравнение
имеет ровно два различных корня.
Решение. Запишем уравнение в виде
и решим его. Первый множитель обнуляется только при 
Второй дает уравнение:
Итого потенциально есть три корня, но некоторые из них могут быть посторонними. Разберем несколько случаев.
Если 
то получаем корни 
и Все в порядке.
Если 
то 
посторонний. Значит, 
и 
не должны быть посторонними или совпадать. То есть 
(иначе не определен логарифм), 
(то есть 
) и 
(иначе не определен корень). Получаем в итоге 
Если 
то посторонний. Значит, и не должны быть посторонними или совпадать. То есть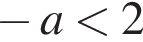 
(иначе не определен логарифм), 
(то есть 
) и 
(иначе не определен корень). Получаем в итоге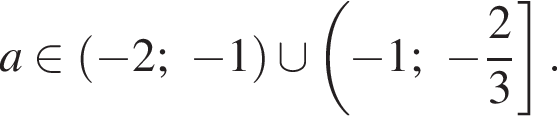 
Окончательный ответ 
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получен ответ, но в решении допущена вычислительная ошибка или оно недостаточно обосновано | 3 |
| С помощью верного рассуждения получен ответ, но в ходе решения допущена одна ошибка, отличная от вычислительной | 2 |
| Получены некоторые верные значения параметра, однако решение содержит более одной ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |