В правильной четырехугольной призме 
АВ = ВС = 8, 
Через точки А и С перпендикулярно 
проведена плоскость Ω.
а) Докажите, что плоскость Ω пересекает ребро 
в такой точке М, что 
б) Найдите угол между плоскостями Ω и 
Решение. а) Введем координаты с началом в точке A и осями, направленными по ребрам AB, AD,
соответственно. Тогда координаты некоторых точек будут такими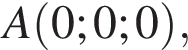 
Тогда вектор 
и уравнение перпендикулярной к нему плоскости имеет вид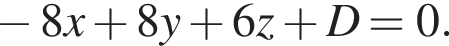 
Чтобы плоскость проходила через точку A, нужно чтобы 
Заметим, что 
действительно проходит и через точку 
Обозначим координаты точки пересечения T этой плоскости с за 
Тогда 
то есть 
Тогда 
и 
б) Уравнение плоскости 
это 
(ясно, что точки A, C, 
в него подходят), поэтому
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |