РЕШУ ЕГЭ — математика профильная

Задания

Тип Д17 C6 № 521229 Добавить в вариант

Источник: А. Ларин: Тренировочный вариант № 191

Классификатор алгебры: Неравенства с параметром

Сложные задачи с параметром. Неравенства с параметром

Найдите все значения параметра а, при каждом из которых уравнение

$левая круглая скобка ax минус a минус 2 правая круглая скобка умножить на левая круглая скобка левая круглая скобка ax минус a минус 2 правая круглая скобка в квадрате плюс 1 правая круглая скобка = дробь: числитель: левая круглая скобка a минус 10x правая круглая скобка умножить на левая круглая скобка левая круглая скобка a минус 10x правая круглая скобка в квадрате плюс левая круглая скобка x минус 1 правая круглая скобка в квадрате правая круглая скобка , знаменатель: левая круглая скобка x минус 1 правая круглая скобка в кубе конец дроби$

имеет ровно два различных действительных корня.

Решение. Введем функцию $f левая круглая скобка x правая круглая скобка =x левая круглая скобка x в квадрате плюс 1 правая круглая скобка =x в кубе плюс x.$ Уравнение примет вид:

$f левая круглая скобка ax минус a минус 2 правая круглая скобка =f левая круглая скобка дробь: числитель: a минус 10x, знаменатель: x минус 1 конец дроби правая круглая скобка .$

Поскольку $f левая круглая скобка x правая круглая скобка$ монотонно возрастает (ее производная $f' левая круглая скобка x правая круглая скобка =3x в квадрате плюс 1 больше 0$ ), это возможно в том и только том случае, когда $ax минус a минус 2= дробь: числитель: a минус 10x, знаменатель: x минус 1 конец дроби .$ Значит, именно это уравнение должно иметь два корня. Имеем:

$ax минус a минус 2= дробь: числитель: a минус 10x, знаменатель: x минус 1 конец дроби равносильно левая круглая скобка ax минус a минус 2 правая круглая скобка левая круглая скобка x минус 1 правая круглая скобка =a минус 10x.$ $ax минус a минус 2= дробь: числитель: a минус 10x, знаменатель: x минус 1 конец дроби равносильно$
$равносильно левая круглая скобка ax минус a минус 2 правая круглая скобка левая круглая скобка x минус 1 правая круглая скобка =a минус 10x.$

При этом $x=1$ не должно быть корнем. Оно является корнем при $левая круглая скобка минус 2 правая круглая скобка умножить на 0=a минус 10,$ то есть при $a=10.$

$ax в квадрате минус ax минус ax плюс a минус 2x плюс 2 минус a плюс 10x=0 равносильно$
$равносильно ax в квадрате плюс левая круглая скобка 8 минус 2a правая круглая скобка x плюс 2=0.$

При $a=0$ получаем $8x плюс 2=0,$ один корень. При прочих a это квадратное уравнение, вычислим дискриминант:

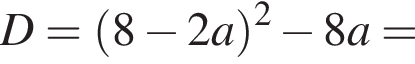
$D= левая круглая скобка 8 минус 2a правая круглая скобка в квадрате минус 8a=$
$=64 минус 40a плюс 4a в квадрате =4 левая круглая скобка a минус 2 правая круглая скобка левая круглая скобка a минус 8 правая круглая скобка больше 0$ при $a меньше 2$ или $a больше 8.$

Получаем ответ: 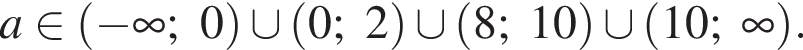$a принадлежит левая круглая скобка минус бесконечность ;0 правая круглая скобка \cup левая круглая скобка 0;2 правая круглая скобка \cup левая круглая скобка 8;10 правая круглая скобка \cup левая круглая скобка 10; бесконечность правая круглая скобка .$

Ответ: $левая круглая скобка минус бесконечность ;0 правая круглая скобка \cup левая круглая скобка 0;2 правая круглая скобка \cup левая круглая скобка 8;10 правая круглая скобка \cup левая круглая скобка 10; плюс бесконечность правая круглая скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен правильный ответ.	4
Получен верный ответ. Решение в целом верное. Обосновано найдены оба промежутка значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность.	3
Обосновано найден хотя бы один промежуток значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность.	2
Решение содержит: − или верное описание расположения двух лучей и прямой из условия задачи; − или верное получение квадратного уравнения с параметром a относительно одной из переменных.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	4

521229

$левая круглая скобка минус бесконечность ;0 правая круглая скобка \cup левая круглая скобка 0;2 правая круглая скобка \cup левая круглая скобка 8;10 правая круглая скобка \cup левая круглая скобка 10; плюс бесконечность правая круглая скобка .$

Источник: А. Ларин: Тренировочный вариант № 191

Классификатор алгебры: Неравенства с параметром

Ключ

№ п/п	№ задания	Ответ
1	521229	$левая круглая скобка минус бесконечность ;0 правая круглая скобка \cup левая круглая скобка 0;2 правая круглая скобка \cup левая круглая скобка 8;10 правая круглая скобка \cup левая круглая скобка 10; плюс бесконечность правая круглая скобка .$