i
Взяли последовательность первых 15 натуральных чисел.
а) Можно ли эти числа разбить на 5 групп так, что бы суммы чисел стоящих в одной группе имели разные остатки при делении на 5?
б) Можно ли эти числа разбить на 7 групп так, что бы суммы чисел входящих в одну группу имели разные остатки при делении на 7?
в) Можно ли эти числа упорядочить таким образом, что бы суммы любых трех последовательных чисел делилась на 5?
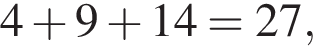
Поэтому общая сумма делилась бы на 7.
Если 
и 
делятся на 5, то и 
делится на 5. То есть числа a и d дают одинаковые остатки от деления на 5, если стоят через два числа друг от друга. Но тогда числа с номерами 1, 4, 7, 10, 13 дают одинаковые остатки от деления на 5, что невозможно — там нет пяти чисел с одинаковыми остатками.